
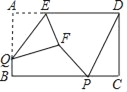
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是____.
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米![]()
(1)设平均每天的工作量为x(单位:万米![]() ),用
),用![]() 来表示运输公司完成任务所需的时间,并写出x的取值范围.
来表示运输公司完成任务所需的时间,并写出x的取值范围.
(2)由于工程进度的需要,实际平均每天运送土石方是原计划的1.2倍,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少米![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
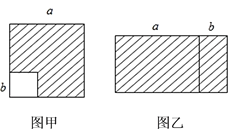
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
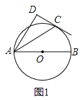
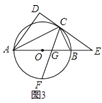
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
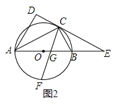
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,又过
,又过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 为
为![]() ,则下列说法:①
,则下列说法:①![]() 是
是![]() 的中点;②
的中点;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤连接
为等腰三角形;⑤连接![]() ,若
,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为24;其中正确的是______(填序号).
的面积为24;其中正确的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
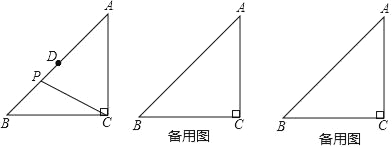
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com