
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,又过
,又过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 为
为![]() ,则下列说法:①
,则下列说法:①![]() 是
是![]() 的中点;②
的中点;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤连接
为等腰三角形;⑤连接![]() ,若
,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为24;其中正确的是______(填序号).
的面积为24;其中正确的是______(填序号).

【答案】③④⑤
【解析】
根据等腰三角形的定义、三角形的中线、三角形的高的概念进行判断,对角线垂直的四边形的面积=对角线乘积的一半;分别对选项进行判断,即可得到答案.
解:∵AD是![]() 的平分线,
的平分线,
假设①![]() 是
是![]() 的中点成立,则AB=AC,即△ABC是等腰三角形;显然△ABC不一定是等腰三角形,故①错误;
的中点成立,则AB=AC,即△ABC是等腰三角形;显然△ABC不一定是等腰三角形,故①错误;
根据题目的条件,不能证明![]() ,故②错误;
,故②错误;
∵∠ADC=∠1+∠ABD,∠1=∠2,
∴∠ADC>∠2,故③正确;
∵∠1=∠2,AH=AH,∠AHF=∠AHC=90°,
∴△AHF≌△AHC(ASA),
∴AF=AC,故④正确;
∵AD⊥CF,
∴S四边形ACDF=![]() ×AD×CF=
×AD×CF=![]() ×6×8=24.故⑤正确;
×6×8=24.故⑤正确;
∴正确的有:③④⑤;
故答案为:③④⑤.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
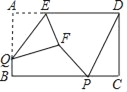
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
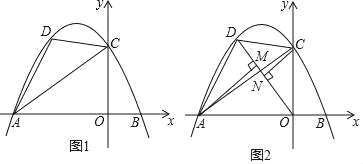
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
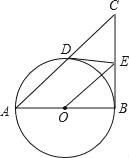
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
(1)证明OE∥AD;
(2)①当∠BAC= °时,四边形ODEB是正方形.
②当∠BAC= °时,AD=3DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
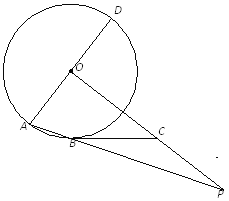
【题目】如图,AD是⊙O的直径,AB为⊙O 的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
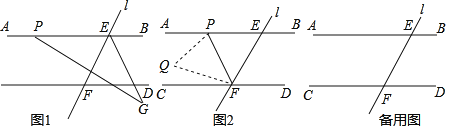
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点)
(1)若∠CFE=119°,PG交∠FEB的平分线EG于点G,∠APG=150°,则∠G的大小为 .
(2)如图2,连接PF.将△EPF折叠,顶点E落在点Q处.
①若∠PEF=48°,点Q刚好落在其中的一条平行线上,请直接写出∠EFP的大小为 .
②若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场上有一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
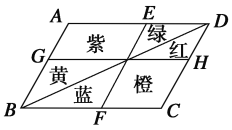
A. 红花、绿花种植面积一定相等
B. 紫花、橙花种植面积一定相等
C. 红花、蓝花种植面积一定相等
D. 蓝花、黄花种植面积一定相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com