
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
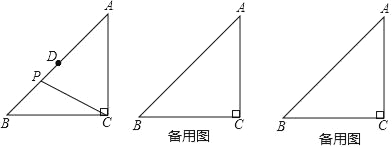
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
【答案】(1)PC=3;(2)![]() 或
或![]() ;(3)4+
;(3)4+![]() .
.
【解析】
![]() 如图1中,连接CD.D是AB的中点,可求出CD,再根据勾股定理求出PC;
如图1中,连接CD.D是AB的中点,可求出CD,再根据勾股定理求出PC;
![]() 当△BPC是等腰三角形时,分三种情形讨论;
当△BPC是等腰三角形时,分三种情形讨论;
![]()
![]() 推出点P落在CD的延长线与⊙D的交点处,PC的值最大,推出
推出点P落在CD的延长线与⊙D的交点处,PC的值最大,推出![]() 可得AB′的最大值为
可得AB′的最大值为![]() .
.
(1)如图1中,连接CD.
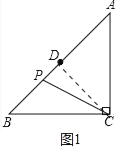
在Rt△ABC中,∠ACB=90°,AC=BC=4,
∴AB=![]() ,
,
∵AD=DB,
∴CD=![]() AB=
AB=![]() ,CD⊥AB,
,CD⊥AB,
在![]() 中,
中,![]()
(2)如图2中,
![]()
∴点P在以点D为圆心的⊙D上.
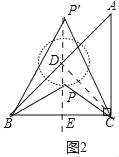
①当PB=PC时,
∵CD=DB,
∴P、D都在线段BC的垂直平分线上,设直线DP交BC于E.
∴∠PEC=90°,BE=CE=2,
∵∠CDB=90°,
∴DE=![]() BC=CE=2,
BC=CE=2,
在![]() 中,
中,![]()
当P在线段PD上时,PE=DE﹣DP=1,![]()
当P在线段ED的延长线上时,PE=ED+DP=3,![]()
②当PC=BC时,![]()
∴PC≠BC,此种情形不存在;
③当PB=BC时,同理这种情形不存在;
如图3中
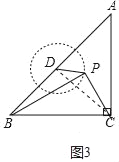
(3)如图4中,连接BB′.
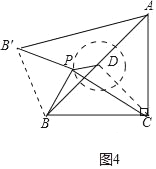
由旋转可知:PB=PB′,∠BPB′=90°,
∴∠PBB′=45°,
∴BB′=![]() PB,
PB,
∴![]()
∵AC=BC,∠ACB=90°,
∴∠ABC=45°,
∴∠ABC=∠PBB′,
∴∠ABB′=∠CBP,
∵![]()
∴![]()
∴![]()
∴△ABB′∽△CBP,
∴![]()
![]()
∴点P落在CD的延长线与⊙D的交点处,PC的值最大,
![]()
∴AB′的最大值为4+![]() .
.


科目:初中数学 来源: 题型:
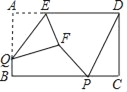
【题目】如图,矩形ABCD中,AB=4,BC=8,P,Q分别是直线BC,AB上的两个动点,AE=2,△AEQ沿EQ翻折形成△FEQ,连接PF,PD,则PF+PD的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
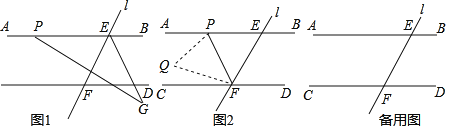
【题目】如图1,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点)
(1)若∠CFE=119°,PG交∠FEB的平分线EG于点G,∠APG=150°,则∠G的大小为 .
(2)如图2,连接PF.将△EPF折叠,顶点E落在点Q处.
①若∠PEF=48°,点Q刚好落在其中的一条平行线上,请直接写出∠EFP的大小为 .
②若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2nx﹣n2+n的顶点为P,直线y=![]() 分别交x,y轴于点M,N.
分别交x,y轴于点M,N.
(1)若点P在直线MN上,求n的值;
(2)是否存在过(0,﹣2)的直线与抛物线交于A,B两点(A点在B点的下方),使AB为定长,若存在,求出AB的长;若不存在,请说明理由;
(3)在(2)的条件下,当四边形MABN的周长最小时,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药厂两年前生产1t某种药品的成本是5000元,随着生产技术的进步,现在生产1t该种药品的成本是3000元.设该种药品生产成本的年平均下降率为x,则下列所列方程正确的是( )
A. 5000×2(1﹣x)=3000 B. 5000×(1﹣x)2=3000
C. 5000×(1﹣2x)=3000 D. 5000×(1﹣x2)=3000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,同时在甲服装店租用2件和乙服装店租用3件共需280元,在甲服装店租用4件和乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,则超出5件的部分可按原价的六折进行优惠;设需要租用![]() (
(![]() )件服装,选择甲店则需要
)件服装,选择甲店则需要![]() 元,选择乙店则需要
元,选择乙店则需要![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广场上有一个形状是平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法错误的是( )
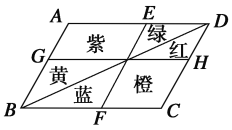
A. 红花、绿花种植面积一定相等
B. 紫花、橙花种植面积一定相等
C. 红花、蓝花种植面积一定相等
D. 蓝花、黄花种植面积一定相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com