
【题目】某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):

设参加旅游的员工人数为x人.
(1)当25<x<40时,人均费用为 元,当x≥40时,人均费用为 元;
(2)该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?
【答案】(1)1000﹣20(x﹣25);700.(2)30名
【解析】
(1)求出当人均旅游费为700元时的员工人数,再根据给定的收费标准即可求出结论;
(2)由25×1000<27000<40×700可得出25<x<40,由总价=单价×数量结合(1)的结论,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.
解:(1)∵25+(1000﹣700)÷20=40(人),
∴当25<x<40时,人均费用为[1000﹣20(x﹣25)]元,当x≥40时,人均费用为700元.
(2)∵25×1000<27000<40×700,
∴25<x<40.
由题意得:x[1000﹣20(x﹣25)]=27000,
整理得:x2﹣75x+1350=0,
解得:x1=30,x2=45(不合题意,舍去).
答:该单位这次共有30名员工去旅游.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是菱形(四条边都相等的平行四边形).AB=4,∠ABC=60°,∠EAF的两边分别与边BC,DC相交于点E,F,且∠EAF=60°.
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系为: .
(2)如图2,当点E是线段CB上任意一点时(点E不与B,C重合),求证:BE=CF;
(3)求△AEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
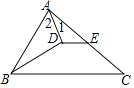
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l:y=﹣![]() x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
(1)写出S与m之间的函数表达式,并写出m的取值范围.
(2)当S=3时,求点P的坐标.
(3)若直线OP平分△AOB的面积,求点P的坐标.
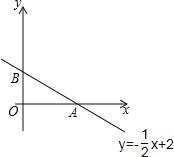
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
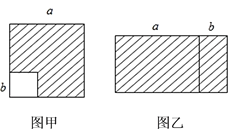
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的k个数:x1,x2,…,xk,称为数列Ak:x1,x2,…,xk,其中k为整数且k≥3.
定义V(Ak)=|x1﹣x2|+|x2﹣x3|+…+|xk﹣2﹣xk﹣1|+|xk﹣1﹣xk|.
例如,若数列A5:1,2,3,4,5,则V(A5)=|1﹣2|+|2﹣3|+|3﹣4|+|4﹣5|=4.
根据以上材料,回答下列问题:
(1)已知数列A3:3,5,﹣2,求V(A3).
(2)已知数列A4:x1,x2,x3,x4,其中x1,x2,x3,x4为4个互不相等的整数,且x1=3,x4=7,V(A4)=4,直接写出满足条件的数列A4.
(3)已知数列A5:x1,x2,x3,x4,x5中的5个数均为非负整数,且x1+x2+x3+x4+x5=25,请直接写出V(A5)的最大值和最小值及对应的数列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为点
的切线互相垂直,垂足为点![]() .
.
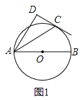
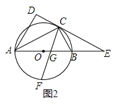
![]() 如图
如图![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
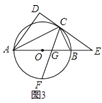
![]() 如图
如图![]() ,直线
,直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,如图
的条件下,如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com