
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的k个数:x1,x2,…,xk,称为数列Ak:x1,x2,…,xk,其中k为整数且k≥3.
定义V(Ak)=|x1﹣x2|+|x2﹣x3|+…+|xk﹣2﹣xk﹣1|+|xk﹣1﹣xk|.
例如,若数列A5:1,2,3,4,5,则V(A5)=|1﹣2|+|2﹣3|+|3﹣4|+|4﹣5|=4.
根据以上材料,回答下列问题:
(1)已知数列A3:3,5,﹣2,求V(A3).
(2)已知数列A4:x1,x2,x3,x4,其中x1,x2,x3,x4为4个互不相等的整数,且x1=3,x4=7,V(A4)=4,直接写出满足条件的数列A4.
(3)已知数列A5:x1,x2,x3,x4,x5中的5个数均为非负整数,且x1+x2+x3+x4+x5=25,请直接写出V(A5)的最大值和最小值及对应的数列.
【答案】(1)9(2)数列A4为:3,4,5, 7;3,4,6,7;3,5,4,7;3,5,6,7;3,6,4,7;3,6,5,7(3)5,5,5,5,5
【解析】
(1)根据定义V(Ak)=|x1﹣x2|+|x2﹣x3|+…+|xk﹣1﹣xk|,代入数据即可求出结论;(2)在数轴上标出x1、x4表示的点,利用数形结合可得出x2、x3在3到7之间,找出所有的搭配方式,即可求解;(3)由数列A5:x1,x2,x3,x4,x5中5个数均为非负数,结合绝对值即可得出0≤V(A5)≤25,由此即可求解.
(1)V(A3)=|3﹣5|+|5﹣(﹣2)|=2+7=9;
(2)V(A4)=|3﹣x2|+|x2﹣x3|+|x3﹣7|=4可看成3条线段的长度和,如图所示.
![]()
∵7﹣3=4,
∴x2、x3在3到7之间,
∵x1,x2,x3,x4为4个互不相等的整数,
∴数列A4为:3,4,5, 7;3,4,6,7;3,5,4,7;3,5,6,7;3,6,4,7;3,6,5,7.
(3)∵x1,x2,x3,x4,x5中5个数均为非负数,假设x1≥x2≥x3≥x4≥x5,
∴x1≥|x1﹣x2|,x2≥|x2﹣x3|,x3≥|x3﹣x4|,x4≥|x4﹣x5|,x5≥0,
∴0≤|x1﹣x2|+|x2﹣x3|+|x3﹣x4|+|x4﹣x5|≤x1+x2+x3+x4+x5,即0≤V(A5)≤25.
∴V(A5)的最大值为25,对应的数列为:25,0,0,0,0或0,0,0,0,25或0,25,0,0,0或0,0,25,0,0或0,0,0,25,0,
最小值为0,对应的数列为5,5,5,5,5.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】问题探究
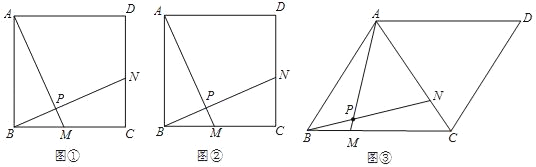
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):

设参加旅游的员工人数为x人.
(1)当25<x<40时,人均费用为 元,当x≥40时,人均费用为 元;
(2)该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
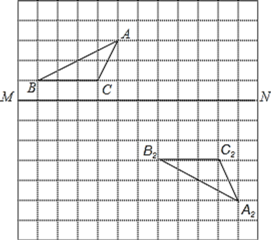
【题目】在如图所示的方格纸中.
(1)作出![]() 关于
关于![]() 对称的图形
对称的图形![]() .
.
(2)说明![]() ,可以由
,可以由![]() 经过怎样的平移变换得到?
经过怎样的平移变换得到?
(3)以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 的中点为坐标原点,建立直角坐标系,试在
的中点为坐标原点,建立直角坐标系,试在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 最小(保留找点
最小(保留找点![]() 的作图痕迹,描出点
的作图痕迹,描出点![]() 的位置,并写出点
的位置,并写出点![]() 的坐标).
的坐标).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个村庄A、B在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,CD=3千米.现要在河边CD上建造一水厂,向A、B两村送自来水.铺设水管的工程费用为每千米20000元,请你在CD上选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用W.

查看答案和解析>>
科目:初中数学 来源: 题型:
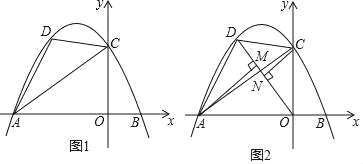
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com