
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
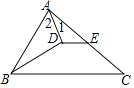
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
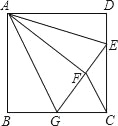
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
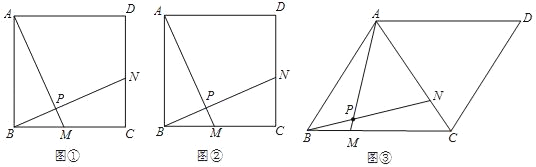
【题目】问题探究
(1)如图①,已知正方形ABCD的边长为4.点M和N分别是边BC、CD上两点,且BM=CN,连接AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.
(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,求△APB周长的最大值;
问题解决
(3)如图③,AC为边长为2![]() 的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
的菱形ABCD的对角线,∠ABC=60°.点M和N分别从点B、C同时出发,以相同的速度沿BC、CA向终点C和A运动.连接AM和BN,交于点P.求△APB周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
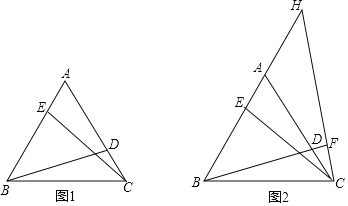
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
12×231=132×21,
13×341=143×31
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25
② ×396=693× ;
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并证明;
(3)若(2)中a,b表示一个两位数,例如a=11,b=22,则1122×223311=113322×2211,请写出表示这类“数字对称等式”一般规律的式子(含a,b),并写出a+b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位准备组织员工到武夷山风景区旅游,旅行社给出了如下收费标准(如图所示):

设参加旅游的员工人数为x人.
(1)当25<x<40时,人均费用为 元,当x≥40时,人均费用为 元;
(2)该单位共支付给旅行社旅游费用27000元,请问这次参加旅游的员工人数共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
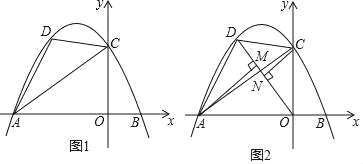
【题目】已知,如图1,直线y=![]() x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为
x+3与x轴、y轴分别交于A、C两点,点B在x轴上,点B的横坐标为![]() ,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
,抛物线经过A、B、C三点.点D是直线AC上方抛物线上任意一点.
(1)求抛物线的函数关系式;
(2)若P为线段AC上一点,且S△PCD=2S△PAD,求点P的坐标;
(3)如图2,连接OD,过点A、C分别作AM⊥OD,CN⊥OD,垂足分别为M、N.当AM+CN的值最大时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com