
【题目】观察下列等式:
12×231=132×21,
13×341=143×31
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”
(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:
①52× = ×25
② ×396=693× ;
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a,b),并证明;
(3)若(2)中a,b表示一个两位数,例如a=11,b=22,则1122×223311=113322×2211,请写出表示这类“数字对称等式”一般规律的式子(含a,b),并写出a+b的取值范围.
【答案】(1)①275,572;②63,36;(2)(10a+b)[100b+10(a+b)+a]=[100a+10(a+b)+b](10b+a),证明见解析;(3)22≤a+b≤99
【解析】
(1)观察几行等式发现规律,根据规律求解即可;
(2)根据两位数的个位数字、十位数字、个位数与十位数之和分别是三位数的百位上的数、个位上的数、十位上的数,即可写出等式;
(3)通过观察可知,![]() 、
、![]() 都是个位与十位数字相等的两位数,且
都是个位与十位数字相等的两位数,且![]() ,则
,则![]() ,由此规律写出只含
,由此规律写出只含![]() 、
、![]() 的规律的式子,再由
的规律的式子,再由![]() 得
得![]() 的取值范围.
的取值范围.
解:(1)观察可知:若两位数的个位数字、十位数字、个位数与十位数之和分别是三位数的百位上的数字、个位上的数字、十位上的数字,这样的两位数与三位数的积,则等于这个三位数与两位数各自交换个位数字与十位数字所得的三位数与两位数的积,
∴①![]()
②![]() .
.
故答案为:①![]() 、
、![]() ;②
;②![]() 、
、![]() .
.
(2)![]()
验证:等式左边![]()
等式右边![]()
左边=右边.
答:表示“数字对称等式”一般规律的式子为:![]() ;
;
(3)规律:若![]() ,
,![]() ,(m、n均为1至8的自然数),且
,(m、n均为1至8的自然数),且![]() ,则
,则![]() .
.![]() 的取值范围为:
的取值范围为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民在枯水期(当年11月至第二年5月)节约用电,规定7:00至23:00为用电高峰期,此期间用电电费y1(单位:元)与用电量x(单位:度)之间满足的关系如图所示;规定23:00至第二天早上7:00为用电低谷期,此期间用电电费y2(单位:元)与用电量x(单位:元)之间满足如表所示的一次函数关系.
(1)求y2与x的函数关系式;并直接写出当0≤x≤180和x>180时,y1与x的函数关系式;

(2)若市民王先生一家在12月份共用电350度,支付电费150元,求王先生一家在高峰期和低谷期各用电多少度.
低谷期用电量x度 | … | 80 | 100 | 140 | … |
低谷期用电电费y2元 | … | 20 | 25 | 35 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
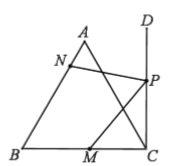
【题目】如图,点![]() 在等边
在等边![]() 的边
的边![]() 上,
上,![]() ,射线
,射线![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 是射线
是射线![]() 上一动点,点
上一动点,点![]() 是线段
是线段![]() 上一动点,当
上一动点,当![]() 的值最小时,
的值最小时,![]() ,则
,则![]() 的长为___________________.
的长为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
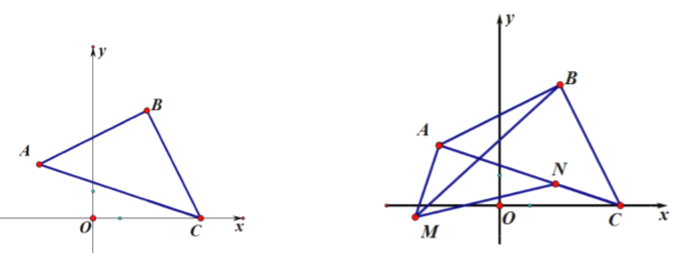
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,且
,且 ![]() ,
,![]() 满足
满足![]() .
.
(1)写出![]() 、
、![]() 两点坐标;
两点坐标;
(2)求![]() 点坐标;
点坐标;
(3)如图,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,请写出线段
,请写出线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
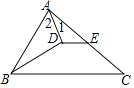
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l:y=﹣![]() x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
(1)写出S与m之间的函数表达式,并写出m的取值范围.
(2)当S=3时,求点P的坐标.
(3)若直线OP平分△AOB的面积,求点P的坐标.
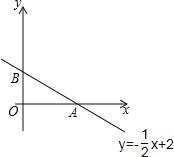
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com