
【题目】如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
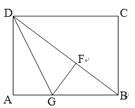
(1)求证:△ADG≌△FDG;(2)若BG=2AG,BD=2![]() ,求AD的长.
,求AD的长.
【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】试题分析:(1)由矩形的性质和已知条件得出∠A=∠GFD,∠ADG=∠FDG,由AAS即可证明△AGD≌△FGD;
(2)由△AGD≌△FGD,得出对应边相等FG=AG,根据BG=2AG求出∠FBG=30°,根据直角三角形中30° 的角所对的边是斜边的一半即可求出.
试题解析:
(1)证明:∵四边形ABCD是矩形,GF⊥BD,
∴∠A=∠DFG=90°,
又∠ADG=∠FDG,DG=DG,
∴△ADG≌△FDG.
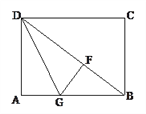
(2)解:由(1)得△ADG≌△FDG,
∴FG=AG,
∵BG=2AG,∴BG=2FG,
∴在Rt△BFG中,sin∠FBG=![]() ,
,
∴∠FBG=30°,
∴AD=![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB及CB延长线交于点F、M.
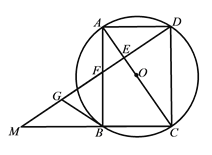
(1)求证:四边形ABCD是矩形;
(2)若点G为MF的中点,求证:BG是⊙O的切线;
(3)若AD=4,CM=9,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在进行“阳光体育活动”中,统计了7位原来偏胖的学生的情况,他们的体重分别降低了5,9,3,10,6,8,5(单位:kg),则这组数据的中位数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
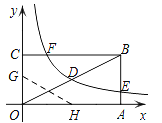
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=﹣![]() , 下列说法不正确的是( )
, 下列说法不正确的是( )
A.图象经过点(1,﹣1)
B.图象在第二、四象限
C.x>0时,y随x的增大而增大
D.x<0时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com