
分析 根据方程组的解即为函数图象的交点坐标解答.
解答 解:∵一次函数y=-mx+4和y=3x-n的图象交于点P(3,1),
∴方程组 $\left\{\begin{array}{l}{mx+y=4}\\{3x-y=n}\end{array}\right.$的解是 $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
故答案为:$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$
点评 本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
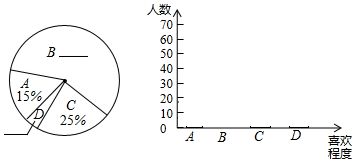 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表. | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
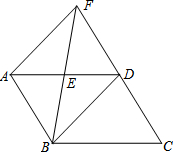 如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.
如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com