
 如图,已知一次函数${y_1}=\frac{2}{3}x+b$与反比例函数${y_2}=\frac{k}{x}$的图象交于A(3,4)、B(-6,n)两点.
如图,已知一次函数${y_1}=\frac{2}{3}x+b$与反比例函数${y_2}=\frac{k}{x}$的图象交于A(3,4)、B(-6,n)两点.分析 (1)把点A坐标代入反比例函数求出k的值,也就求出了反比例函数解析式;
(2)根据图象和交点坐标即可求得;
(3)把点A的坐标代入${y_1}=\frac{2}{3}x+b$,求得一次函数解析式,求出直线与y轴的交点坐标,从而y轴把△AOB分成两个三角形,结合点A、B的横坐标分别求出两个三角形的面积,相加即可.
解答 解:(1)点A(3,4)在反比例函数${y_2}=\frac{k}{x}$的图象上,
∴k=3×4=12,
∴反比例函数的表达式为y2=$\frac{12}{x}$,
(2)一次函数值小于反比例函数值的x的取值范围是x<-6或0<x<3;
(3)把点A(3,4)代入一次函数${y_1}=\frac{2}{3}x+b$中,
得4=$\frac{2}{3}$×3+b,
解得b=2,
∴一次函数的表达式为y1=$\frac{2}{3}$x+2;
当x=0时,得y=2,
∴直线y1=$\frac{2}{3}$x+2与y轴的交点为C(0,2),
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×2×6+$\frac{1}{2}$×2×3=9.
点评 本题考查了反比例函数与一次函数图象的交点问题,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.


科目:初中数学 来源: 题型:选择题
 如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )
如图所示,二次函数y=-x2+2x+k的图象与x轴的一个交点坐标为(3,0),则关于x的一元二次方程-x2+2x+k=0的解为( )| A. | x1=3,x2=-2 | B. | x1=3,x2=-1 | C. | x1=1,x2=-1 | D. | x1=3,x2=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 南偏东50° | B. | 南偏西50° | C. | 北偏东50° | D. | 北偏西50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
| A. | 8 | B. | 9 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平方根是本身的数为0、1 | |
| B. | 0.125的立方根是$\frac{1}{2}$ | |
| C. | 无限小数是无理数,无理数也是无限小数 | |
| D. | 一个无理数和一个有理数之积为无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
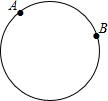 如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.
如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com