
 ①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;
①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;分析 ①根据条件画出图形,分两种情况:i)当C在B的右侧时,如图1,有AC+BC=7;ii)当C在A的左侧时,如图2,分别列式得出结论;
②先计算方程的最小值,当x在m和n之间时,k最小,最小值就是m和n的距离m-n,把k分三种情况讨论:当0<k<m-n时,原方程无解;当k=m-n时,解为:n≤x≤m,当k>m-n时,分x在m的右侧和n的左侧讨论,列式得出方程的解.
解答 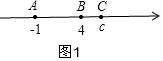 解:①∵点A、B在数轴上分别表示-1、4,
解:①∵点A、B在数轴上分别表示-1、4,
∴AB=5,
∵点C到点A、B的距离之和是7,
∴C不可能在A、B之间,
分两种情况:i)当C在B的右侧时,如图1,有AC+BC=7,
则c+1+c-4=7,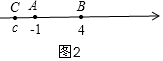
c=5;
ii)当C在A的左侧时,如图2,有AC+BC=7,
则-1-c+4-c=7,
c=-2,
综上所述,c的值为5或-2;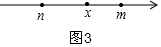
故答案为:5或-2;
②由题意可知:|x-m|+|x-n|的最小值为|m-n|=m-n,
当0<k<m-n时,原方程无解;
当k=m-n时,原方程的解为:n≤x≤m,如图3,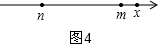
当k>m-n时,分两种情况:i)当x>m时,如图4,x-m+x-n=k,
2x=k+m+n,
x=$\frac{1}{2}$(k+m+n),
ii)当x<n时,如图5,m-x+n-x=k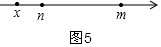 ,
,
2x=m+n-k,
x=$\frac{1}{2}$(m+n-k),
此时原方程的解为:x1=$\frac{1}{2}$(k+m+n),x2=$\frac{1}{2}$(m+n-k).
点评 本题考查了数轴上两点的距离与绝对值的关系,知道数轴上两点的距离等于两点坐标之差的绝对值,且某点A到另外两点B和C的距离和有最小值,最小值是该点A在这两点之间时,即最小值为BC的长.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
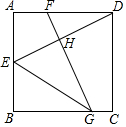 已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H.
已知:如图,正方形ABCD中,E是AB上一点,FG⊥DE于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com