
【题目】如图,长方形ABCD的顶点A、B分别在x轴、y轴上,OA=OB=2,AD=4![]() ,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为( )
,将长方形ABCD绕点O顺时针旋转,每次旋转90°,则第2021次旋转结束时,点C的坐标为( )

A.(6,4)B.(4,6)C.(-6,4)D.(-4,6)
【答案】A
【解析】
先求出C点坐标,根据OC点绕原点旋转,找出规律即可求解.
如图,过点C作CE⊥y轴于点E,连接OC,
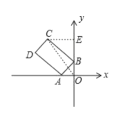
∵OA=OB=2
∴∠ABO=∠BAO=45°,
∵∠ABC=90°
∴∠CBE=45,
∵BC=AD=![]() ,
,
∴CE=BE=4,
∴OE=OB+BE=6,
∴C(-4,6),
∵矩形ABCD绕点O顺时针旋转,每次旋转90°,
则第1次旋转结束时,点C的坐标为(6,4);
第2次旋转结束时,点C的坐标为(4,-6);
则第3次旋转结束时,点C的坐标为(-6,-4);
则第4次旋转结束时,点C的坐标为(-4,6);
……
发现规律:旋转4次一个循环,
∴2021÷4=505…1,
则第2021次旋转结束时,点C的坐标为(6,4),
故选:A.


科目:初中数学 来源: 题型:
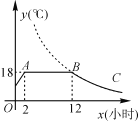
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为方便顾客停车,决定设计一个地下停车场,为了测得该校地下停车场的限高CD,在施工时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园广播主持人培训班开展比赛活动,分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,对应的成绩分别是
四个等级,对应的成绩分别是![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,根据下图不完整的统计图解答下列问题:
分,根据下图不完整的统计图解答下列问题:
(1)补全下面两个统计图(不写过程);
(2)求该班学生比赛的平均成绩;
(3)现准备从等级![]() 的
的![]() 人(两男两女)中随机抽取两名主持人,请利用列表或画树状图的方法,求恰好抽到一男一女学生的概率?
人(两男两女)中随机抽取两名主持人,请利用列表或画树状图的方法,求恰好抽到一男一女学生的概率?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形纸片ABCD,AB=4,BC=10,M是BC的中点,点P沿折线BA—AD运动,以MD为折瘪将长方形纸片向右翻折,使点B落在长方形的AD边上,则折痕MP的长______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点A、B、C、D对应的数分别是a、b、c、d,且d﹣2a=14

(1)那么a= ,b= ;
(2)点A以3个单位/秒的速度沿着数轴的正方向运动,1秒后点B以4个单位/秒的速度也沿着数轴的正方向运动.当点A到达D点处立刻返回,与点B在数轴的某点处相遇,求这个点对应的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】余姚某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低1元,则平均每天的销量可增加10千克.(销售利润=销售价—进价)
(1)如果每千克核桃降价![]() 元,那么每千克核桃的销售利润为________元,平均每天可销售_________千克;(用含
元,那么每千克核桃的销售利润为________元,平均每天可销售_________千克;(用含![]() 的代数式表示)
的代数式表示)
(2)若该专卖店销售这种核桃想要平均每天获利2240元,每千克核桃应降价多少元?
(3)在(2)条件下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com