
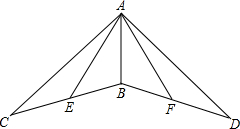
 如图,在△ABC与△ABD中,BC=BD,点E为BC中点,点F为BD中点,连接AE,AF,AE=AF.求证:∠C=∠D.
如图,在△ABC与△ABD中,BC=BD,点E为BC中点,点F为BD中点,连接AE,AF,AE=AF.求证:∠C=∠D. 分析 根据SSS证明△ABE与△ABF全等,得出∠ABE=∠ABF,再利用SAS证明△ABC与△ABD全等即可.
解答 证明:∵BC=BD,点E为BC中点,点F为BD中点,
∴BE=BF,
在△ABE与△ABF中,
$\left\{\begin{array}{l}{AB=AB}\\{AE=AF}\\{BE=BF}\end{array}\right.$,
∴△ABE≌△ABF(SSS),
∴∠ABE=∠ABF,
在△ABC与△ABD中
$\left\{\begin{array}{l}{AB=AB}\\{∠ABE=∠ABF}\\{BC=BD}\end{array}\right.$,
∴△ABC≌△ABD(SAS),
∴∠C=∠D.
点评 本题主要考查对全等三角形的判定的理解和掌握,能熟练地运用全等三角形的判定定理进行证明是解此题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A′B′,BC=B′C′,∠C=∠C′ | |
| B. | ∠B=135°,∠B′=135°,AB=B′C′,BC=C′A′ | |
| C. | AB=BC=CA,A′B′=B′C′=C′A′,∠A=∠A′ | |
| D. | AB=A′B′,BC=B′C′,∠B=∠B′=135° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
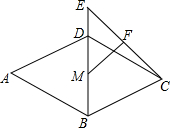 已知:如图,菱形ABCD的边长为4,∠A=60°,M是对角线BD的中点,延长BD到点E,连接EC,F是EC的中点
已知:如图,菱形ABCD的边长为4,∠A=60°,M是对角线BD的中点,延长BD到点E,连接EC,F是EC的中点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解旬河水中汞含量是否符合规定标准 | |
| B. | 了解县师训教研中心36名员工的健康状况 | |
| C. | 商家为了解某一批“电子白板”的使用寿命 | |
| D. | 为了解空气中PM2.5含量 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3 | B. | a≤3 | C. | a>3 | D. | a≥3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com