
分析 直接应用:根据a+b≥2$\sqrt{ab}$得到y1+y2=2x+$\frac{2}{x}$≥2$\sqrt{2x•\frac{2}{x}}$,于是得到2x=$\frac{2}{x}$时,y1+y2的最小值为4,然后求出x的值;
实际应用:先得到每小时耗油量($\frac{x}{18}$+$\frac{450}{x}$)升,利用题中的不等式得到$\frac{x}{18}$+$\frac{450}{x}$≥2$\sqrt{\frac{x}{18}•\frac{450}{x}}$,于是得到当$\frac{x}{18}$=$\frac{450}{x}$时,$\frac{x}{18}$+$\frac{450}{x}$的最小值为10,然后求出对应x的值;
变形应用:先计算出$\frac{{y}_{2}}{{y}_{1}}$=x+1+$\frac{4}{x+1}$,利用题中的不等式得到x+1+$\frac{4}{x+1}$≥2$\sqrt{(x+1)•\frac{4}{x+1}}$,于是得到x+1=$\frac{4}{x+1}$时,x+1+$\frac{4}{x+1}$的最小值为4,然后解方程x+1=$\frac{4}{x+1}$求出满足条件的x的值.
解答 解:直接应用:y1+y2=2x+$\frac{2}{x}$≥2$\sqrt{2x•\frac{2}{x}}$,即当2x=$\frac{2}{x}$时,y1+y2的最小值为4,此时x=1;
故答案为1,4;
实际应用:每小时耗油量为x($\frac{1}{18}$+$\frac{450}{{x}^{2}}$)=$\frac{x}{18}$+$\frac{450}{x}$,而$\frac{x}{18}$+$\frac{450}{x}$≥2$\sqrt{\frac{x}{18}•\frac{450}{x}}$,所以当$\frac{x}{18}$=$\frac{450}{x}$时,$\frac{x}{18}$+$\frac{450}{x}$的最小值为10,此时x=90,
所以该小汽车为每小时90公理时,每小时耗油量最少,最小值为10升;
变形应用:$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+4}{x+1}$=x+1+$\frac{4}{x+1}$,而x+1+$\frac{4}{x+1}$≥2$\sqrt{(x+1)•\frac{4}{x+1}}$,所以x+1=$\frac{4}{x+1}$时,x+1+$\frac{4}{x+1}$的最小值为4,此时x=1,
所以当x=1时,$\frac{{y}_{2}}{{y}_{1}}$的最小值为4.
点评 本题考查了配方法的应用:利用配方法求二次三项式是一个完全平方式时所含字母系数的值,关键是:二次三项式是完全平方式,则常数项是一次项系数一半的平方;记住若a≥0,b≥0时,a+b≥2$\sqrt{ab}$.当且仅当a=b时,“=”成立.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
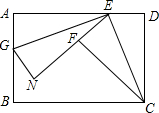 如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.
如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com