
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
【考点】根的判别式;根与系数的关系.
【专题】计算题.
【分析】(1)先计算出△=(m+2)2﹣4(2m﹣1),变形得到△=(m﹣2)2+4,由于(m﹣2)2≥0,则△>0,然后根据△的意义得到方程有两个不相等的实数根;
(2)利用根与系数的关系得到x1+x2=0,即m+2=0,解得m=﹣2,则原方程化为x2﹣5=0,然后利用直接开平方法求解.
【解答】(1)证明:△=(m+2)2﹣4(2m﹣1)
=m2﹣4m+8
=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
即△>0,
所以方程有两个不相等的实数根;
(2)设方程的两个根为x1,x2,由题意得:
x1+x2=0,即m+2=0,解得m=﹣2,
当m=﹣2时,方程两根互为相反数,
当m=﹣2时,原方程为x2﹣5=0,
解得:x1=﹣ ,x2=
,x2= .
.
【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2﹣4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了解一元二次方程和根与系数的关系.


科目:初中数学 来源: 题型:
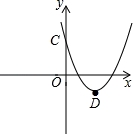
已知二次函数y=x2﹣2mx+m2﹣1(m≠0)的图象经过点(1,0).
(1)求二次函数的解析式;
(2)该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
( 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将4×3的网格图剪去5个小正方形后,图中还剩下7个小正方形,为了使余下的部分(小正方形之间至少要有一条边相连)恰好能折成一个正方体,需要再剪去1个小正方形,则应剪去的小正方形的编号是( )
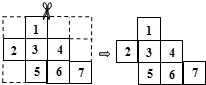
A.7 B.6 C.5 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图一,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1︰0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是 ……………………………………………………………………( )
 (A)0.55; (B)0.8;
(A)0.55; (B)0.8;
(C)0.6; (D)0.75.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com