
已知二次函数y=x2﹣2mx+m2﹣1(m≠0)的图象经过点(1,0).
(1)求二次函数的解析式;
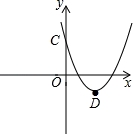
(2)该抛物线与y轴交于点C,顶点为D,求C,D两点的坐标;
( 3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
3)x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.
【考点】二次函数综合题.
【分析】(1)把点(1,0)代入y=x2﹣2mx+m2﹣1,解方程求出m的值即可;
(2)令x=0,得y=3,即可得出C点坐标.将抛物线解析式配方成顶点式,即可得出顶点D的坐标;
(3)由两点之间线段最短知PC+PD≤CD,得出当C,P,D三点共线时,PC+PD最短.由待定系数法求出直线CD的解析式,即可求出点P坐标.
【解答】解:(1)把点(1,0)代入y=x2﹣2mx+m2﹣1,
得:12﹣2m+m2﹣1=0,
解得:m=2,或m=0(不合题意,舍去),
∴m=2,
∴二次函数的解析式为y=x2﹣4x+3;
(2)令x=0,得y=3,
∴C点坐标为(0,3).
将y=x2﹣4x+3配方得:y=(x﹣2)2﹣1,
∴D点坐标为(2,﹣1).
(3)存在;点P的坐标为(1.5,0).理由如下:
由两点之间线段最短知PC+PD≤CD,
∴当C,P,D三点共线时,PC+PD最短.
设直线CD的解析式为y=kx+b,
根据题意得: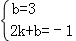 ,
,
解得:k=﹣2,b=3,
直线CD的解析式为:y=﹣2x+3,
当y=0时,x=1.5,
∴点P的坐标为(1.5,0).
【点评】本题是二次函数综合题目,考查了二次函数解析式的求法、一次函数解析式的求法、抛物线的顶点坐标、抛物线与y轴的交点、最短线段问题等知识;本题综合性强,有一定难度,确定二次函数和一次函数解析式是解决问题的关键.


科目:初中数学 来源: 题型:
在2010年上海世博会期间,某超市在销售中发现:吉祥物﹣“海宝”平均每天可售出20套,每件盈利40元.国庆长假商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套.要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )

A.21 B.24 C.27 D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
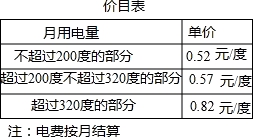
为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
若某户居民1月份用电250度,则应收电费:0.52×200+0.57×(250﹣200)=132.5元.
(1)若某户居民10月份电费78元,则该户居民10月份用电__________度;
(2)若该户居民2月份用电340度,则应缴电费__________元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com