

分析 (1)分两种情况利用三角形的面积公式可以表示出0$≤t<2\sqrt{3}$时重叠部分的面积,当2$\sqrt{3}$≤t≤6时用△ABC的面积-△BEH的面积即可求出重叠部分的面积;
(2)当点A与点D重合时,BE=CE=2$\sqrt{3}$,再由条件可以求出AN的值,分三种情况讨论求出AH的值,①AN=AH=4时,②AN=NH=4时,此时H点在线段AG的延长线上,③AH=NH时,此时H点为线段AG的中垂线与AG的交点,从而可以求出答案.
解答 解:(1)如图1所示.
当0≤t<2$\sqrt{3}$时,
∵△ABC为等边三角形,
∴∠HCE=60°.
∴$\frac{EH}{EC}=\sqrt{3}$.
∴EC=t,EH=$\sqrt{3}t$.
∴△HEC的面积=$\frac{1}{2}EC•EH$=$\frac{1}{2}×t×\sqrt{3}t$=$\frac{\sqrt{3}}{2}{t}^{2}$.
如图2所示:
过点A作AM⊥BC,垂足为M.
当2$\sqrt{3}$≤t≤6时,EC=t,则BE=4$\sqrt{3}$-t,
∵△ABC为等边三角形,
∴∠B=60°.
∴$\frac{HE}{BE}=\sqrt{3}$.
∴HE=$\sqrt{3}$BE,即EH=$\sqrt{3}×(4\sqrt{3}-t)$.
∴△BHE的面积=$\frac{1}{2}BE•EH=\frac{1}{2}×\sqrt{3}×(4\sqrt{3}-t)^{2}$.
过点A作AM⊥BC,垂足为M.
∴$\frac{AM}{AB}=\frac{\sqrt{3}}{2}$,即$\frac{AM}{4\sqrt{3}}=\frac{\sqrt{3}}{2}$.
∴AM=6.
∴△ABC的面积=$\frac{1}{2}CB•AM=\frac{1}{2}×4\sqrt{3}×6$=12$\sqrt{3}$.
∴重合部分的面积=S△ABC-S△BHE=-$\frac{\sqrt{3}}{2}{t}^{2}+12t-12\sqrt{3}$.
∴S与t之间的函数关系式为S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{t}^{2}(0≤t<2\sqrt{3})}\\{-\frac{\sqrt{3}}{2}{t}^{2}+12t-12\sqrt{3}(2\sqrt{3}≤t≤6)}\end{array}\right.$.
(2)①当AH=AN时,如图3所示.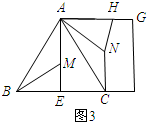
∵当点A与点D重合时,
∴BE=CE=2$\sqrt{3}$.
∵BM平分∠ABE,
∴$∠MBE=\frac{1}{2}∠ABE=30°$.
∴ME=2.
∵∠ABM=∠BAM.
∴AM=BM=4.
∵△ABM≌△ACN,
∴∠CAN=30°,AN=4.
∴AH=4;
②如图4所示;过点N作NK⊥AG,垂足为K.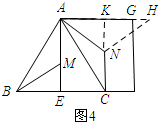
当AN=NH=4时,此时H点在线段AG的延长线上.
∵∠EAC=∠CAN=30°,
∴∠KAN=30°.
∴AK=$\frac{\sqrt{3}}{2}×AN$=$\frac{\sqrt{3}}{2}×4=2\sqrt{3}$.
∵AN=NH,NK⊥AH,
∴AK=KH.
∴AH=2AK=4$\sqrt{3}$.
③当AH=NH时,如图5所示;过点H作HK⊥AN,垂足为K.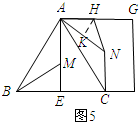
∵AH=HN,KH⊥AN,
∴AK=KN.
∴AK=$\frac{1}{2}AN=2$.
∴AH=$\frac{AK}{cos∠HAK}=\frac{4\sqrt{3}}{3}$.
点评 本题考查了求函数的解析式,正方形的性质,全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质,勾股定理的运用,根据题意画出符合题意的图形是解答本题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题
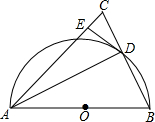 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD.过点D作DE⊥AC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
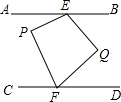 已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.
已知AB∥CD,P是AB、CD之间的一点,E、F分别是AB、CD上的定点,连接PE、PF,如图,在AB、CD之间另取一点Q,使∠PEQ=2∠BEQ,∠PFQ=2∠QFD,当∠P=∠Q时,判断PE、PF的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com