练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，△ABC平移得到△DEF，并且DE由线段AB平移而得，AB=BC=4cm，DF=5cm．则△DEF的周长是13cm．

    分析 根据平移的性质，线段DE是由线段AB平移而得，线段EF由线段BC平移而得，则AB=DE，BC=EF，结合已知可求△DEF的周长．

    解答 解：∵线段DE是由线段AB平移而得，
    ∴DE=AB=4cm，
    同理，EF=BC=4cm，
    又DF=5cm，
    ∴△DEF的周长=DE+EF+DF=4+5+4=13cm．
    故答案是：13cm．

    点评 本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图AB∥CD，AC平分∠BAD，BD平分∠ADC，AC和BD交于点E，F为AD的中点，连结EF．
    （1）找出图中所有的等腰三角形，并证明其中的一个；
    （2）若AE=8，DE=6，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

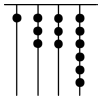    1．我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）
    A．517B．84C．336D．1326

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在直角△ABC中，∠C=90°，∠A=35°，以直角顶点C为旋转中心，将△ABC旋转到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于点D，这时∠BDC的度数是105°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若$\frac{a}{ab+a+1}$+$\frac{b}{bc+b+1}$+$\frac{c}{ca+c+1}$=1，则abc=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．对于正实数a，b；（$\frac{a+b}{2}$）2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=（$\frac{a-b}{2}$）2
    ∵（$\frac{a-b}{2}$）2≥0；∴ab≤（$\frac{a+b}{2}$）2；如图：如果点A（a，b）是反比例函数y=$\frac{3}{x}$（x＞0）图象上一点，过点A作x轴的垂线；过点A作y轴的垂线，垂足分别为点B，C，仿照上面给定的条件
    （1）求出四边形OBAC的周长最小值
    （2）四边形OBAC的周长最小时点A的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．一个均匀的正方体般子，六个面分别标有数字1，2，3，4，5，6．抛掷这个骰子记正面朝上的数字为a．能使命题“对于二次函数y=mx2-5mx+1（m是常数，m＜0），当x＜a时y随x的增大而增大”为真命题的概率是$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

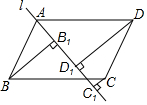    19．如图，过?ABCD的顶点A作直线l．
    （1）若l交BC边于点E，BB1⊥AE，CC1⊥AE，DD1⊥AE，B1，C1，D1为垂足，求证：BB1+CC1=DD1
    （2）若l交CD于点E，BB1⊥AE，CC1⊥AE，DD1⊥AE，B1，C1，D1为垂足，试探究BB1，CC1，DD1之间的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．把下列各数填在相应的表示集合的大括号里：
    -$\frac{2}{3}$，12，-（-96），-|-3|，-4.5，0，|-2.5|，$\frac{1}{3}$
    （1）整数集合{12，-（-96），-|-3|，0}
    （2）负数集合{-$\frac{2}{3}$，-|-3|，-4.5}
    （3）正分数集合{|-2.5|，$\frac{1}{3}$}
    （4）有理数集合{-$\frac{2}{3}$，12，-（-96），-|-3|，-4.5，0，|-2.5|，$\frac{1}{3}$}．

    查看答案和解析>>

    同步练习册答案