
 ������ʵ��a��b����$\frac{a+b}{2}$��2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=��$\frac{a-b}{2}$��2
������ʵ��a��b����$\frac{a+b}{2}$��2-ab=$\frac{{a}^{2}+2ab+{b}^{2}}{4}$-$\frac{4ab}{4}$=$\frac{{a}^{2}-2ab+{b}^{2}}{4}$=��$\frac{a-b}{2}$��2���� ��1���ɵ�A�ڵ�һ�����ɵó�a��0��b��0��a+b��0��ab=3�����ab�ܣ�$\frac{a+b}{2}$��2���ɵó�a+b��2$\sqrt{3}$���ٸ��ݾ��ε��ܳ���ʽ���ɵó����ۣ�
��2���ɵ�a=bʱa-b=0�����ɵó���a=bʱ�ı���OBAC���ܳ���С�����ab=3���ɵó���A�����꣮
��� �⣺��1���ߵ�A��a��b���Ƿ���������y=$\frac{3}{x}$��x��0��ͼ����һ�㣬
��a��0��b��0��a+b��0��ab=3��
��ab�ܣ�$\frac{a+b}{2}$��2��
��a+b��2$\sqrt{3}$��
���ı���OBAC���ܳ�2��a+b����4$\sqrt{3}$�����ı���OBAC���ܳ���СֵΪ4$\sqrt{3}$��
��2���ߵ�a=bʱ��a-b=0��
�൱a=bʱ���ı���OBAC���ܳ���С��
��ab=3���ҵ�A��a��b���ڵ�һ���ޣ�
���ı���OBAC���ܳ���Сʱ��A������Ϊ��$\sqrt{3}$��$\sqrt{3}$����
���� ���⿼���˷���������ͼ���ϵ����������������ʽ�������Լ����ε��ܳ�������Ĺؼ��ǣ���1�����ݲ���ʽ�������ҳ�a+b��2$\sqrt{3}$����2�����ݲ���ʽ�������ҳ���a=bʱ���ı���OBAC���ܳ���С��


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $2\sqrt{10}$ | B�� | 12 | C�� | 2$\sqrt{10}$+10 | D�� | 12��2$\sqrt{10}$+10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a-8}{5}$���� | B�� | $\frac{a+8}{5}$���� | C�� | $\frac{a-4}{5}$���� | D�� | $\frac{a-16}{5}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
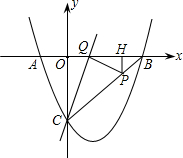 ��ͼ����֪������y=$\frac{3}{4}{x}^{2}$+bx+c���ύ��A��B���㣬��y�ύ��C�㣬A������Ϊ��-1��0��������C��ֱ��y=$\frac{3}{4t}$x-3��x�ύ�ڵ�Q����P���߶�BC�ϵĶ��㣬��P��PH��OB�ڵ�H����PB=5t����0��t��1��
��ͼ����֪������y=$\frac{3}{4}{x}^{2}$+bx+c���ύ��A��B���㣬��y�ύ��C�㣬A������Ϊ��-1��0��������C��ֱ��y=$\frac{3}{4t}$x-3��x�ύ�ڵ�Q����P���߶�BC�ϵĶ��㣬��P��PH��OB�ڵ�H����PB=5t����0��t��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABCƽ�Ƶõ���DEF������DE���߶�ABƽ�ƶ��ã�AB=BC=4cm��DF=5cm�����DEF���ܳ���13cm��
��ͼ����ABCƽ�Ƶõ���DEF������DE���߶�ABƽ�ƶ��ã�AB=BC=4cm��DF=5cm�����DEF���ܳ���13cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
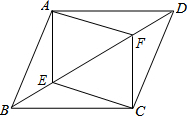 ��ͼ�����ı���ABCD�У���E��F�ǶԽ���BD�ϵ����㣬��BE=DF��
��ͼ�����ı���ABCD�У���E��F�ǶԽ���BD�ϵ����㣬��BE=DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com