Question

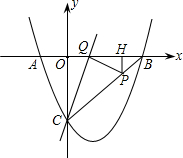
3．如图，已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点，与y轴交于C点，A的坐标为（-1，0），过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q，点P是线段BC上的动点，过P作PH⊥OB于点H．若PB=5t，且0＜t＜1．
（1）求点C的坐标及抛物线的解析式；
（2）求线段QH的长（用含t的式子表示）；
（3）依点P的变化，是否存在t的值，使△CPQ为直角三角形，若存在，请直接写出t的值，不存在，说明理由．

Answer 1

分析 （1）先利用一次函数解析式确定C（0，-3），然后利用待定系数法求抛物线解析式；
（2）利用抛物线与x轴的交点问题，求出B（4，0），则利用勾股定理可表示出BC=5，再表示出Q（4t，0），接着证明△BPH∽△BCO，则利用相似可表示出BH=4t，讨论：当0＜t≤$\frac{1}{2}$时，QH=4-8t；当$\frac{1}{2}$＜t＜1时，QH=8t-4；
（3）先利用勾股定理表示出PH=3t，只有0＜t＜$\frac{1}{2}$时，△CPQ可能为直角三角形，若∠CQP=90°，证明△COQ∽△QPH；若∠QPC=90°，易得△PHQ∽△BHP，然后分别利用相似比可确定满足条件t的值．

解答 解：（1）当x=0时，y=$\frac{3}{4t}$x-3=-3，则C（0，-3），
把A（-1，0），C（0，-3）代入y=$\frac{3}{4}{x}^{2}$+bx+c得$\left\{\begin{array}{l}{\frac{3}{4}-b+c=0}\\{c=-3}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=-\frac{9}{4}}\\{c=-3}\end{array}\right.$，
所以抛物线解析式为y=$\frac{3}{4}{x}^{2}$-$\frac{9}{4}$x-3；
（2）当y=0时，$\frac{3}{4}{x}^{2}$-$\frac{9}{4}$x-3=0，解得x₁=-1，x₂=4，则B（4，0），
∴BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
当y=0时，y=$\frac{3}{4t}$x-3=0，解得x=4t，则Q（4t，0），
∵PH∥CO，
∴△BPH∽△BCO，
∴$\frac{BH}{BO}$=$\frac{BP}{BC}$，即$\frac{BH}{4}$=$\frac{5t}{5}$，解得BH=4t，
当0＜t≤$\frac{1}{2}$时，QH=OB-OQ-BH=4-8t；
当$\frac{1}{2}$＜t＜1时，QH=8t-4；
（3）存在．当0＜t＜$\frac{1}{2}$时，存在t的值使△CPQ为直角三角形，
在Rt△BPH中，PH=$\sqrt{（5t）^{2}-（4t）^{2}}$=3t，
若∠CQP=90°，∵∠CQO+∠QCO=90°，∠CQO+∠PQH=90°，
∴∠QCO=∠PQH，
∴△COQ∽△QPH，
∴$\frac{OQ}{PH}$=$\frac{OC}{QH}$，即$\frac{4t}{4-8t}$=$\frac{3}{3t}$，解得t₁=-1+$\sqrt{2}$，t₂=-1-$\sqrt{2}$（舍去），
若∠QPC=90°，易得△PHQ∽△BHP，
∴PH²=HQ•HB，即（3t）²=（4-8t）•4t，解得t₁=$\frac{16}{41}$，t₂=0（舍去），
综上所述，t的值为-1+$\sqrt{2}$或$\frac{16}{41}$时，△CPQ为直角三角形．

点评 本题考查了二次函数的综合题：熟练掌握待定系数法求二次函数解析式；会求二次函数、一次函数与坐标轴的交点坐标；能运用勾股定理和相似比计算线段的长或表示线段之间的关系；会运用分类讨论的思想解决数学问题．