练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和，如23=3+5，33=7+9+11，43=13+15+17+19，…，若m3分裂后，其中有一个奇数是123，则m的值是（ ）
    A.9
    B.10
    C.11
    D.12

    【答案】C
    【解析】解：∵底数是2的分裂成2个奇数，底数为3的分裂成3个奇数，底数为4的分裂成4个奇数，

    ∴m3有m个奇数，

    ∵2n+1=123，n=61，

    ∴奇数123是从3开始的第6112﹣1个奇数，

    ∵ =54， =65，

    ∴第61个奇数是底数为11的数的立方分裂的奇数的其中一个，

    即m=11．

    故答案为：C．

    根据规律得到底数是2的分裂成2个奇数，底数为3的分裂成3个奇数，底数为4的分裂成4个奇数；得到方程，求出m的值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为支持国家南水北调工程建设，小王家由原来养殖户变为种植户，经市场调查得知，种植草莓不超过20亩时，所得利润y（元）与种植面积m（亩）满足关系式y=1500m；超过20亩时，y=1380m+2400．而当种植樱桃的面积不超过15亩时，每亩可获得利润1800元；超过15亩时，每亩获得利润z（元）与种植面积x（亩）之间的函数关系如下表（为所学过的一次函数、反比例函数或二次函数中的一种）．

    （1）设小王家种植x亩樱桃所获得的利润为P元，直接写出P关于x的函数关系式，并写出自变量的取值范围；

    （2）如果小王家计划承包40亩荒山种植草莓和樱桃，当种植樱桃面积x（亩）满足0＜x＜20时，求小王家总共获得的利润w（元）的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小聪是个数学爱好者，他发现从1开始，连续几个奇数相加，和的变化规律如右表所示：

    加数个数

    连续奇数的和S

    1

    1=

    2

    1+3=22

    3

    1+3+5=32

    4

    1+3+5+7=42

    5

    1+3+5+7+9=52

    n

    …


    （1）如果n=7，则S的值为；
    （2）求1+3+5+7+…+199的值；
    （3）求13+15+17+…+79的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P(1，－2)在平面直角坐标系中所在的象限是( )

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：C是线段AB所在平面内任意一点，分别以AC、BC为边，在AB同侧作等边三角形ACE和BCD，联结AD、BE交于点P．

    （1）如图1，当点C在线段AB上移动时，线段AD与BE的数量关系是： ．
    （2）如图2，当点C在直线AB外，且∠ACB＜120°，上面的结论是否还成立？若成立请证明，不成立说明理由．
    （3）在（2）的条件下，∠APE大小是否随着∠ACB的大小发生变化而发生变化，若变化写出变化规律，若不变，请求出∠APE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，点M是边BC的中点，AD平分∠BAC，BD⊥AD，BD的延长线交AC于点E，AB=12，AC=20．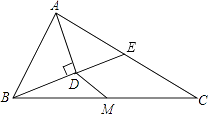
    （1）求证：BD=DE；
    （2）求DM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°．求∠APC度数．
    （1）小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC= ．
    问题迁移：如图3，AD∥BC，点P在射线OM上运动，∠ADP=∠α，∠BCP=∠β．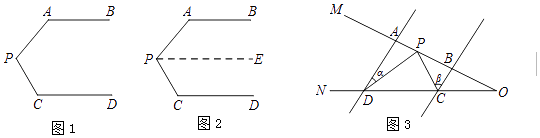

    （2）当点P在A、B两点之间运动时，∠CPD、∠α、∠β之间有何数量关系？请说明理由．
    （3）如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

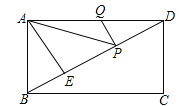
    【题目】如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ的最小值为（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”．
    例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．
    （1）点P（﹣1，6）的“2属派生点”P′的坐标为；
    （2）若点P的“3属派生点”P′的坐标为（6，2），则点P的坐标；
    （3）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

    查看答案和解析>>

    同步练习册答案