
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2属派生点”P′的坐标为;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
【答案】
(1)(11,4)
(2)(0,2)
(3)解:∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka)
∴线段PP′的长为P′到x轴距离为|ka|.
∵P在x轴正半轴,线段OP的长为a,
∴|ka|=2a,即|k|=2,
∴k=±2.
【解析】解:(1)点P(﹣1,6)的“2属派生点”P′的坐标为(﹣1+6×2,﹣1×2+6),即(11,4),
所以答案是:(11,4);
(2)设点P的坐标为(x、y),
由题意知 ![]() ,
,
解得: ![]() ,
,
即点P的坐标为(0,2),
(3)∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka)
∴线段PP′的长为P′到x轴距离为|ka|.
∵P在x轴正半轴,线段OP的长为a,
∴|ka|=2a,即|k|=2,
∴k=±2.
所以答案是:(1)(11,4);(2)(0,2);(3)k=±2.


科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3分裂后,其中有一个奇数是123,则m的值是( )
A.9
B.10
C.11
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我市全面实行新型农村合作医疗,得到了广大农民的积极响应,很多农民看病贵、看病难的问题在合作医疗中得到了缓解.参加医保的农民可在规定的医院就医并按规定标准报销部分医疗费用,表①是医疗费用分段报销的标准;表②是甲、乙、丙三位农民今年的实际医疗费及个人承担总费用.
表①
医疗费用范围 | 门诊费 | 住院费(元) | ||
0~5000的部分 | 5001~20000的部分 | 20001及以上的部分 | ||
报销比例 | a% | 80% | 85% | c% |
表②
门诊费 | 住院费 | 个人承担总费用 | |
甲 | 260元 | 0元 | 182元 |
乙 | 80元 | 2800元 | b元 |
丙 | 400元 | 25000元 | 4030元 |
注明:
①个人承担医疗费=实际医疗费﹣按标准报销的金额;
②个人承担总费用包括门诊费和住院费中个人承担的部分.
③本题中费用精确到元.
请根据上述信息,解答下列问题:
(1)填空:a= , b=;
(2)求住院费20001元及以上的部分报销医疗费用的比例c%;
(3)李大爷去年和今年的实际住院费共计52000元,他本人共承担了6850元,已知今年的住院费超过去年,则李大爷今年实际住院费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,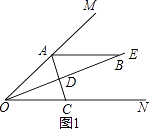
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;
当∠BAD=∠BDA时,x=;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.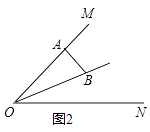
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.
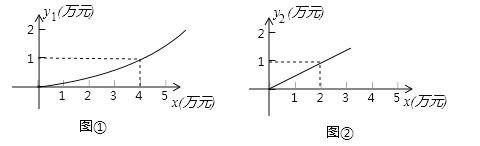
(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com