
【题目】近年来,我市全面实行新型农村合作医疗,得到了广大农民的积极响应,很多农民看病贵、看病难的问题在合作医疗中得到了缓解.参加医保的农民可在规定的医院就医并按规定标准报销部分医疗费用,表①是医疗费用分段报销的标准;表②是甲、乙、丙三位农民今年的实际医疗费及个人承担总费用.
表①
医疗费用范围 | 门诊费 | 住院费(元) | ||
0~5000的部分 | 5001~20000的部分 | 20001及以上的部分 | ||
报销比例 | a% | 80% | 85% | c% |
表②
门诊费 | 住院费 | 个人承担总费用 | |
甲 | 260元 | 0元 | 182元 |
乙 | 80元 | 2800元 | b元 |
丙 | 400元 | 25000元 | 4030元 |
注明:
①个人承担医疗费=实际医疗费﹣按标准报销的金额;
②个人承担总费用包括门诊费和住院费中个人承担的部分.
③本题中费用精确到元.
请根据上述信息,解答下列问题:
(1)填空:a= , b=;
(2)求住院费20001元及以上的部分报销医疗费用的比例c%;
(3)李大爷去年和今年的实际住院费共计52000元,他本人共承担了6850元,已知今年的住院费超过去年,则李大爷今年实际住院费用是多少元?
【答案】
(1)30,616
(2)解:根据表可得丙的住院费用20001元及以上.
根据题意得:400×(1﹣30%)+15000×(1﹣85%)+5000×(1﹣c%)=4030,
解得:c%=90%
(3)解:①当去年住院费是20000元,去年李大爷个人承担费用是5000×(1﹣80%)+15000×(1﹣85%)=3250(元),
今年李大爷个人承担5000×(1﹣80%)+15000×(1﹣85%)+12000×(1﹣90%)=4450(元).
3250+4450>6850;
②当去年住院费是5000元,去年李大爷个人承担费用是5000×(1﹣80%)=1000(元),
今年李大爷个人承担5000×(1﹣80%)+15000×(1﹣85%)+27000×(1﹣90%)=6000(元).
1000+6000>6850;
③当李大爷去年的住院费用在5000元和20000元之间时,设李大爷去年的住院费是x元,则今年的住院费是(52000﹣x)元.
根据题意得:5000×(1﹣80%)+(x﹣5000)×(1﹣85%)+5000×(1﹣80%)+15000×(1﹣85%)+(52000﹣x﹣20000)×(1﹣90%)=6850,
解得:x=3000(不合题意);
总之,李大爷去年的住院费在5000元以下,设去年的住院费是y元,则今年是(52000﹣y)元.
根据题意得:(1﹣80%)y+5000×(1﹣80%)+15000×(1﹣85%)+(52000﹣y﹣20000)×(1﹣90%)=6850,
解得y=4000.
则李大爷今年实际住院费用是52000﹣4000=48000(元).
答:李大爷今年实际住院费用是48000元
【解析】解:(1)a%= ![]() =30%,则a=30;
=30%,则a=30;
乙的住院费用在0~5000的部分.
则b=80×(1﹣30%)+2800×(1﹣80%)=616(元).
故答案是:30,616;
(1)根据题意得到a%的值,求出b的值;(2)根据表可得丙的住院费用20001元及以上,求出报销医疗费用的比例c%的值;(3)根据题意①当去年住院费是20000元,去年李大爷个人承担费用的值和今年李大爷个人承担;②当去年住院费是5000元,求出去年李大爷个人承担费用和今年李大爷个人承担的费用;③当李大爷去年的住院费用在5000元和20000元之间时,求出求出去年李大爷个人承担费用和今年李大爷个人承担的费用;得到李大爷今年实际住院费用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.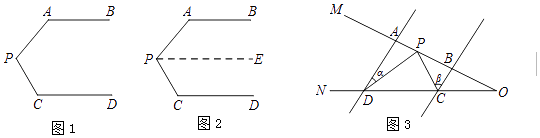
(2)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
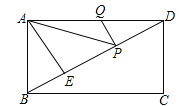
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2属派生点”P′的坐标为;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com