
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,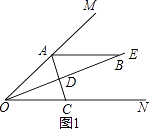
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;
当∠BAD=∠BDA时,x=;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.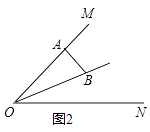
【答案】
(1)18°,126°,63°
(2)解:如图2,存在这样的x的值,使得△ADB中有两个相等的角.
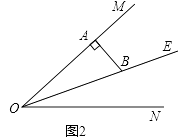
∵AB⊥OM,∠MON=36°,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
①当AC在AB左侧时:
若∠BAD=∠ABD=72°,则∠OAC=90°﹣72°=18°;
若∠BAD=∠BDA=(180°﹣72°)÷2=54°,则∠OAC=90°﹣54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°﹣36°=54°;
②当AC在AB右侧时:
∵∠ABE=108°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=(180°﹣108°)÷2=36°,则∠OAC=90°+36°=126°.
综上所述,当x=18、36、54、126时,△ADB中有两个相等的角.
【解析】解:(1)如图1,①∵∠MON=36°,OE平分∠MON,
∴∠AOB=∠BON=18°,
∵AB∥ON,
∴∠ABO=18°;②当∠BAD=∠ABD时,∠BAD=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°﹣18°×3=126°;③当∠BAD=∠BDA时,∵∠ABO=18°,
∴∠BAD=81°,∠AOB=18°,
∵∠AOB+∠ABO+∠OAB=180°,
∴∠OAC=180°﹣18°﹣18°﹣81°=63°,
(2)如图2,存在这样的x的值,使得△ADB中有两个相等的角.

∵AB⊥OM,∠MON=36°,OE平分∠MON,
∴∠AOB=18°,∠ABO=72°,
①当AC在AB左侧时:
若∠BAD=∠ABD=72°,则∠OAC=90°﹣72°=18°;
若∠BAD=∠BDA=(180°﹣72°)÷2=54°,则∠OAC=90°﹣54°=36°;
若∠ADB=∠ABD=72°,则∠BAD=36°,故∠OAC=90°﹣36°=54°;
②当AC在AB右侧时:
∵∠ABE=108°,且三角形的内角和为180°,
∴只有∠BAD=∠BDA=(180°﹣108°)÷2=36°,则∠OAC=90°+36°=126°.
综上所述,当x=18、36、54、126时,△ADB中有两个相等的角.
所以答案是:(1)①18°;②126°;③63°;(2)当x=18、36、54、126时,△ADB中有两个相等的角.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】已知:C是线段AB所在平面内任意一点,分别以AC、BC为边,在AB同侧作等边三角形ACE和BCD,联结AD、BE交于点P.
(1)如图1,当点C在线段AB上移动时,线段AD与BE的数量关系是: .
(2)如图2,当点C在直线AB外,且∠ACB<120°,上面的结论是否还成立?若成立请证明,不成立说明理由.
(3)在(2)的条件下,∠APE大小是否随着∠ACB的大小发生变化而发生变化,若变化写出变化规律,若不变,请求出∠APE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是 .
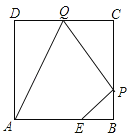
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(﹣1,6)的“2属派生点”P′的坐标为;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.![]()
(1)a= , c=;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b=;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= , 最小值为;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.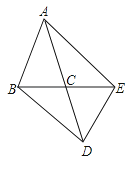
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com