
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.![]()
(1)a= , c=;
(2)如图所示,在(1)的条件下,若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB,则b=;
(3)在(1)(2)的条件下,若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= , 最小值为;
(4)在(1)(2)的条件下,若在点B处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点C处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请表示出甲、乙两小球之间的距离d(用t的代数式表示).
【答案】
(1)-3,9
(2)1
(3)1,12
(4)解:当t不超过4秒(或表述为0≤t≤4或4秒以前),d=12﹣t;
当t超过4秒(或表述为t>4或4秒以后),d=3t﹣4
【解析】解:(1)∵|a+3|+(c﹣9)2=0,
∴a+3=0,c﹣9=0,
解得,a=﹣3,b=9;
⑵数轴上点B表示的数为b.
∵BC=2AB,
∴|c﹣b|=2|b﹣a|,
即9﹣b=2[b﹣(﹣3)]
解得:b=1;
⑶当x=b=1时,
|x﹣a|+|x﹣b|+|x﹣c|=|x﹣(﹣3)|+|x﹣1|+|x﹣9|=12为最小值;
【考点精析】认真审题,首先需要了解数轴(数轴是规定了原点、正方向、单位长度的一条直线),还要掌握代数式求值(求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入)的相关知识才是答题的关键.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】小明一家三口国庆节随旅游团去九寨沟旅游,共花费人民币5600元,他把旅途费用支出情况制成了如下的统计图.请你根据统计图解决下列问题:
(1)哪一部分支出的费用占整个支出的 ![]() ?
?
(2)小明一家在食宿上用去多少元?
(3)小明一家支出的路费共多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF. 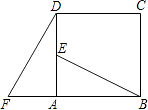
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,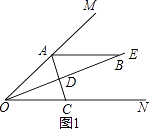
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;
当∠BAD=∠BDA时,x=;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.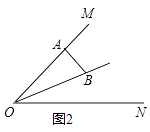
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由若干个完全相同的小正方体堆成的一个几何体放置在平整的地面上.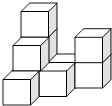
(1)请画出这个几何体的三视图.
(2)如果在这个几何体的表面喷上红色的漆,则在所有的小正方体中,有个小正方体只有一个面是红色,有个小正方体只有两个面是红色,有个小正方体只有三个面是红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.
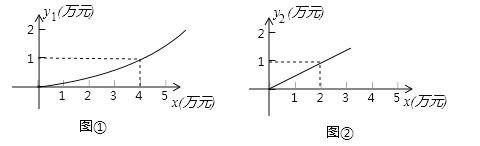
(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
则该函数图象上的点(﹣6,y1),(m2+2m+3,y2)则下列选项正确的是( )
A.y1>y2B.y1≥y2C.y1<y2D.y1≤y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ). 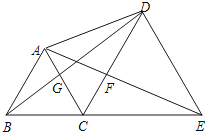
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com