
【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.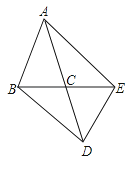
【答案】解:(1)∵△ABC与△DEC关于点C成中心对称,
∴AC=CD,BC=CE,
∴四边形ABDE是平行四边形,
∴AE与BD平行且相等;
(2)∵四边形ABDE是平行四边形,
∴S△ABC=S△BCD=S△CDE=S△ACE ,
∵△ABC的面积为5cm2 ,
∴四边形ABDE的面积=4×5=20cm2;
(3)∠ACB=60°时,四边形ABDE为矩形.
理由如下:∵AB=AC,∠ACB=60°,
∴△ABC是等边三角形,
∴AC=BC,
∵四边形ABDE是平行四边形,
∴AD=2AC,BE=2BC,
∴AD=BE,
∴四边形ABDE为矩形.
【解析】(1)根据中心对称的性质可得AC=CD,BC=CE,然后根据对角线互相平分的四边形是平行四边形得到四边形ABDE是平行四边形,再根据平行四边形的对边互相平行且相等解答;
(2)根据平行四边形的性质,对角线把四边形分成面积相等的四个部分解答;
(3)∠ACB=60°.先判断出△ABC是等边三角形,根据等边三角形的三条边都相等可得AC=BC,然后求出AD=BE,再根据对角线相等的平行四边形是矩形证明.
【考点精析】根据题目的已知条件,利用中心对称及中心对称图形的相关知识可以得到问题的答案,需要掌握如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,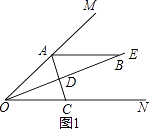
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;
当∠BAD=∠BDA时,x=;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.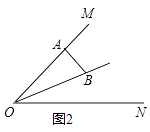
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( ). 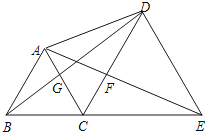
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以只用直尺和圆规作出圆的部分内接正多边形.在我们目前所学知识的范围内,下列圆的内接正多边形不可以用尺规作图作出的是( )
A.正三角形B.正四边形C.正六边形D.正七边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标.
(2)写出顶点B,C,B1 , C1的坐标.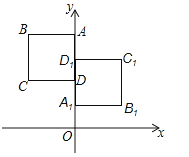
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式![]() (0≤t≤4).
(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数![]() ,
,![]() (
(![]() )当t=
)当t=![]() 或
或![]() 时,足球距离地面的高度都为m(米),求m的取值范围.
时,足球距离地面的高度都为m(米),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】﹣xn与(﹣x)n的正确关系是( )
A.相等
B.互为相反数
C.当n为奇数时它们互为相反数,当n为偶数时相等
D.当n为奇数时相等,当n为偶数时互为相反数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com