
����Ŀ��Ϊ֧�ֹ�����ˮ�������̽��裬С������ԭ����ֳ����Ϊ��ֲ�������г������֪����ֲ��ݮ������20Ķʱ����������y��Ԫ������ֲ���m��Ķ�������ϵʽy=1500m������20Ķʱ��y=1380m+2400��������ֲӣ�ҵ����������15Ķʱ��ÿĶ�ɻ������1800Ԫ������15Ķʱ��ÿĶ�������z��Ԫ������ֲ���x��Ķ��֮��ĺ�����ϵ���±���Ϊ��ѧ����һ�κ�������������������κ����е�һ�֣���

��1����С������ֲxĶӣ������õ�����ΪPԪ��ֱ��д��P����x�ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2�����С���Ҽƻ��а�40Ķ��ɽ��ֲ��ݮ��ӣ�ң�����ֲӣ�����x��Ķ������0��x��20ʱ����С�����ܹ���õ�����w��Ԫ�������ֵ��
���𰸡���1��![]() ����2��61500Ԫ��
����2��61500Ԫ��
��������
�����������1������ͼ�������ʣ����Եó�P����x�ĺ�����ϵʽ�ͳ�x��ȡֵ��Χ��
��2����������=Ķ����ÿĶ���ɵâٵ�0��x��15ʱ�� �ڵ�15��x��20ʱ������ĺ���ʽ�����ö��κ������������ɽ��⣻
�����������1���۲�ͼ����������ϵ�����Եó�P����x�ĺ�����ϵʽΪ��
![]() ��
��
��2��������=Ķ����ÿĶ�������ٵ�0��x��15ʱ��W=1800x+1380��40��x��+2400=420x+55200����x=15ʱ��W�����ֵ��W���=6300+55200=61500��
�ڵ�15��x��20��W=��20x+2100+1380��40��x��+2400=��1400x+59700������1400x+59700��61500����x=15ʱ�����ֵΪ��61500Ԫ��
������������x=15ʱ��W�����ֵ��W���=61500��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н����С�Сѧ�����������г������������д��С�Сѧ����������Ϊ2:3:5������֪��ѧ�����鵽������Ϊ150�ˣ���Ӧ��ȡ���������������� ��
��A��1500 ��B��1000 ��C��150 ��D��500
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���á������һ�������㣺��������������a��b �� �涨a��b=ab2+2ab+a��
�磺1��3=1��32+2��1��3+1=16��
��1����2����3��ֵ��
��2������ ![]() ��3�����
��3����� ![]() ��=8����a��ֵ��
��=8����a��ֵ��
��3����2��x=m �� �� ![]() x����3=n������xΪ�����������ԱȽ�m �� n�Ĵ�С��
x����3=n������xΪ�����������ԱȽ�m �� n�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵxOy�е�λ����ͼ��ʾ������д�����̣�ֱ��д�������
��1������A1B1C1���ABC����ԭ��O�����ĶԳƣ����A1������Ϊ ��
��2������ABC����ƽ��4����λ���ȵõ���A2B2C2�����B2������Ϊ ��
��3������ABC��O��˳ʱ�뷽����ת90�㣬���C�߹���·����Ϊ ��
��4����x������һ��P��ʹPA+PB��ֵ��С�����P������Ϊ ��
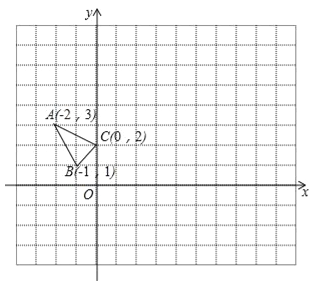
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��k��0����
��k��0����
��1����k=![]() ʱ����������κ����Ķ������ꣻ
ʱ����������κ����Ķ������ꣻ
��2����֤������x��һԪ�η���![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
��3����ͼ���ö��κ�����x�ύ��A��B���㣨A����B�����ࣩ����y�ύ��C�㣬P��y�Ḻ������һ�㣬��OP=1��ֱ��AP��BC�ڵ�Q����֤��![]() ��
��
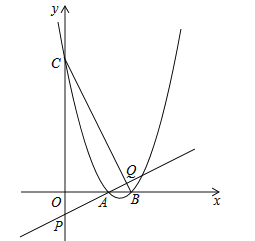
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽��������10 000̨���ӻ���������������г�ȡ100̨���ӻ�����ʵ�飬��������е�����������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��
��![]() ��������
Ϊ��������![]() ����ͼ����A��1��a����B���㣮
����ͼ����A��1��a����B���㣮
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������
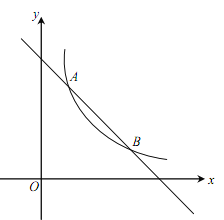
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˳�����������ı��εĸ����е�õ����ı���һ���ǣ� ��
A.������
B.����
C.����
D.ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��������m�������ݿɡ����ѡ������ɸ����������ĺͣ���23=3+5��33=7+9+11��43=13+15+17+19��������m3���Ѻ�������һ��������123����m��ֵ�ǣ� ��
A.9
B.10
C.11
D.12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com