
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
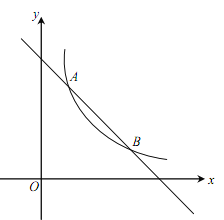
【答案】(1)![]() ,B(3,1);(2)P(
,B(3,1);(2)P(![]() ,0),
,0),![]() .
.
【解析】
试题分析:(1)把点A(1,a)代入一次函数y=﹣x+4,即可得出a,再把点A坐标代入反比例函数![]() ,即可得出k,两个函数解析式联立求得点B坐标;
,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,求出直线AD的解析式,令y=0,即可得出点P坐标.
试题解析:(1)把点A(1,a)代入一次函数y=﹣x+4,得a=﹣1+4,解得a=3,∴A(1,3),点A(1,3)代入反比例函数![]() ,得k=3,∴反比例函数的表达式
,得k=3,∴反比例函数的表达式![]() ,两个函数解析式联立列方程组得
,两个函数解析式联立列方程组得 ,解得
,解得![]() 或
或![]() ,∴点B坐标(3,1);
,∴点B坐标(3,1);
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,∴D(3,﹣1),设直线AD的解析式为y=mx+n,把A,D两点代入得,![]() ,解得m=﹣2,n=5,∴直线AD的解析式为y=﹣2x+5,令y=0,得x=
,解得m=﹣2,n=5,∴直线AD的解析式为y=﹣2x+5,令y=0,得x=![]() ,∴点P坐标(
,∴点P坐标(![]() ,0),S△PAB=S△ABD﹣S△PBD=
,0),S△PAB=S△ABD﹣S△PBD=![]() ×2×2﹣
×2×2﹣![]() ×2×
×2×![]() =2﹣
=2﹣![]() =1.5.
=1.5.


科目:初中数学 来源: 题型:
【题目】已知:菱形ABCD的两条对角线AC,BD交于点O,BE∥AC,CE∥BD. 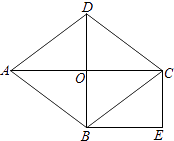
(1)若AC=8,BD=6,求AB的长;
(2)求证:四边形OBEC为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,种植草莓不超过20亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1500m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数、反比例函数或二次函数中的一种).

(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积x(亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
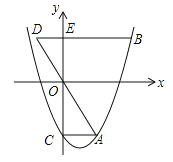
【题目】如图,抛物线![]() (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.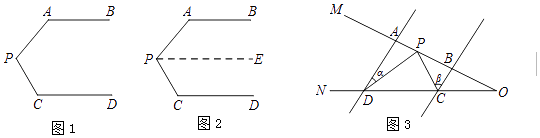
(2)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com