
【题目】已知:菱形ABCD的两条对角线AC,BD交于点O,BE∥AC,CE∥BD. 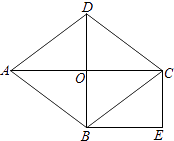
(1)若AC=8,BD=6,求AB的长;
(2)求证:四边形OBEC为矩形.
【答案】
(1)解:∵四边形ABCD是菱形,
∴AC⊥BD,AO= ![]() AC,BO=
AC,BO= ![]() BD,
BD,
∵AC=8,BD=6,
∴AO=4,BO=3,
∴AB= ![]() =5
=5
(2)证明:∵BE∥AC,CE∥BD,
∴四边形OCBD为平行四边形,
∵∠BOC=90°,
∴四边形OBCE为矩形
【解析】(1)利用菱形对角线互相垂直平分和勾股定理计算可得AB的长;(2)易证四边形OCBD是平行四边形,再由∠BOC=90°,即可证明四边形OBEC为矩形
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半),还要掌握矩形的判定方法(有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形)的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.概率很小的事件不可能发生
B.随机事件发生的概率为1
C.不可能事件发生的概率为0
D.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形绕着某一点旋转________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或________,这个点叫做它们的________.这两个图形在旋转后能重合的对应点叫做关于对称中心的________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b , 规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(﹣
☆3)☆(﹣ ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m , ( ![]() x)☆3=n(其中x为有理数),试比较m , n的大小.
x)☆3=n(其中x为有理数),试比较m , n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
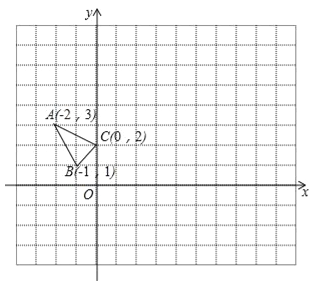
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.(不写解答过程,直接写出结果)
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点B2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点C走过的路径长为 ;
(4)在x轴上找一点P,使PA+PB的值最小,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
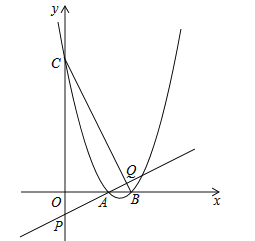
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
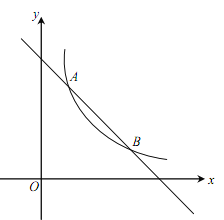
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接春节,某县准备用灯笼美化滨河路,许采用A、B两种不同造型的灯笼共600个.且A型灯笼的数量比B型灯笼的 ![]() 多15个.
多15个.
(1)求A、B两种灯笼各需多少个?
(2)已知A、B型灯笼的单价分别为40元、30元,则这次美化工程需多少费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com