
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数![]() (a,m,c均为常数且ac
(a,m,c均为常数且ac![]() )是“完美抛物线”:
)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=-1,该二次函数图像与y轴交于点C,且![]() .
.
①求a的值;
②当该二次函数图像与端点为M(-1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
【答案】(1)ac<0;
(2)①a的值为1;
②m的取值范围是![]() 或
或![]()
【解析】(1)首先设A点的坐标是(p,q),根据A,B关于原点对称,判断出B点的坐标是(-p,-q);然后根据A,B都是抛物线![]() 上的点,代入求解即可;
上的点,代入求解即可;
(2)①![]() .故a=1.
.故a=1.
②由①可知:抛物线解析式为![]() .MN:
.MN: ![]() (
(![]() ).
).
依题,只需联立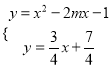 在
在![]() 内只有一个解即可.
内只有一个解即可.
试题解析:(1)设A (p,q).则B (-p,-q).把A、B坐标代入解析式可得:
![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
∵ac![]() .
.
∴![]() .
.
∴ac<0.
(2)∵c=-1.∴![]() ,a>0,且C(0,-1).∴
,a>0,且C(0,-1).∴![]() .
.
①![]() .∴a=1.
.∴a=1.
②由①可知:抛物线解析式为![]() .∵M(-1,1)、N(3,4).
.∵M(-1,1)、N(3,4).
∴MN: ![]() (
(![]() ).
).
依题,只需联立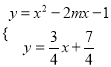 在
在![]() 内只有一个解即可.
内只有一个解即可.
∴![]() .故问题转化为:方程
.故问题转化为:方程![]() 在
在![]() 内只有一个解.
内只有一个解.
建立新的二次函数: ![]() .∵
.∵![]() 且
且![]() .
.
∴抛物线![]() 与x轴有两个交点,且交y轴于负半轴.
与x轴有两个交点,且交y轴于负半轴.
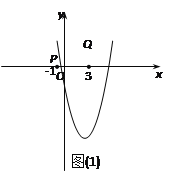
问题进一步转化为抛物线![]() 与x轴的两个交点中,只能有一个点落在以P(-1,0)、Q(3,0)为端点的线段PQ上.
与x轴的两个交点中,只能有一个点落在以P(-1,0)、Q(3,0)为端点的线段PQ上.
分情况讨论:
㈠当抛物线与x轴的左交点落在线段PQ上.则右交点在PQ的延长线上.如图(1):
则对于函数![]() 有
有![]() 即:
即: 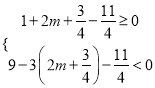 ,
,
解得: ![]() .
.
㈡当抛物线与x轴的右交点落在线段PQ上.则左交点在QP的延长线上.如图(2):
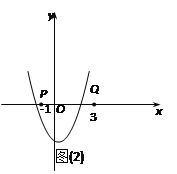
则对于函数![]() 有
有![]()
即: 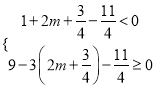 ,解得:
,解得: ![]() .
.
综上所述, ![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
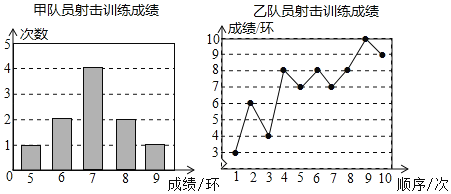
根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=4,BC=3.半径为1的圆的圆心P以1个单位/S的速度由点A沿AC方向在AC上移动,设移动时间为t(单位:s). 
(1)当t为何值时,⊙P与AB相切;
(2)作PD⊥AC交AB于点D,如果⊙P和线段BC交于点E.求当t为何值时,四边形PDBE为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若x1+x2=1﹣x1x2 , 求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥CD,试解决下列问题:
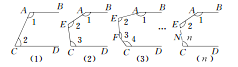
(1)在图(1)中,∠1+∠2等于多少度?请说明理由;
(2)在图(2)中∠1+∠2+∠3等于多少度?请说明理由;
(3)在图(n)中,试探究∠1+∠2+∠3+∠4+…+∠n等于多少度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com