
【题目】如图,△ABC中,∠C=90°,AC=4,BC=3.半径为1的圆的圆心P以1个单位/S的速度由点A沿AC方向在AC上移动,设移动时间为t(单位:s). 
(1)当t为何值时,⊙P与AB相切;
(2)作PD⊥AC交AB于点D,如果⊙P和线段BC交于点E.求当t为何值时,四边形PDBE为平行四边形.
【答案】
(1)解:∵过P作PH⊥AB于H,
又∵⊙P与AB相切,
∴PH=1,
∴∠AHP=∠C=90°,∠A=∠A,
∴△APH∽△ABC,
∴ ![]() ,
,
∵△ABC中,∠C=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∴ ![]() ,
,
∴AP= ![]() ,
,
∴当t= ![]() 时,⊙P与AB相切
时,⊙P与AB相切
(2)解:∵PD⊥AC,∠C=90°,
∴PD∥BE,
∴当PE∥AB时,四边形PDBE为平行四边形.
∴△CPE∽△CAB,
∴ ![]() ,
,
∴ ![]() ,
,
∴CP= ![]() ,
,
∴AP=AC﹣CP= ![]() ,
,
∴当t= ![]() 时,四边形PDBE为平行四边形.
时,四边形PDBE为平行四边形.
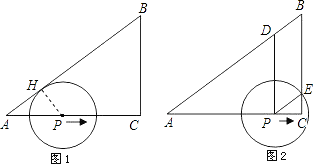
【解析】(1)首先过P作PH⊥AB于H,由⊙P与AB相切,可得PH=1,易证得△APH∽△ABC,根据相似三角形的对应边成比例,可得 ![]() ,继而求得AP的长;即可得当t为何值时,⊙P与AB相切;(2)由PD⊥AC,∠C=90°,可证得PD∥BC,继而可得当PE∥AB时,四边形PDBE为平行四边形,则可得△CPE∽△CAB,然后由相似三角形的对应边成比例,求得CP的长,继而求得答案.
,继而求得AP的长;即可得当t为何值时,⊙P与AB相切;(2)由PD⊥AC,∠C=90°,可证得PD∥BC,继而可得当PE∥AB时,四边形PDBE为平行四边形,则可得△CPE∽△CAB,然后由相似三角形的对应边成比例,求得CP的长,继而求得答案.


科目:初中数学 来源: 题型:
【题目】一个运算程序输入x后,得到的结果是4x3﹣2,则这个运算程序是( )
A.先乘4,然后立方,再减去2
B.先立方,然后减去2,再乘4
C.先立方,然后乘4,再减去2
D.先减去2,然后立方,再乘4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD丄PA,垂足为D. 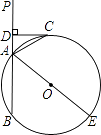
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数![]() (a,m,c均为常数且ac
(a,m,c均为常数且ac![]() )是“完美抛物线”:
)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=-1,该二次函数图像与y轴交于点C,且![]() .
.
①求a的值;
②当该二次函数图像与端点为M(-1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,在与原方向相反的方向上平行行驶,则这两次拐弯的角度应为( )
A. 第一次向右拐38°,第二次向左拐142°
B. 第一次向左拐38°,第二次向右拐38°
C. 第一次向左拐38°,第二次向左拐142°
D. 第一次向右拐38°,第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
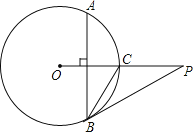
【题目】如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com