
【题目】若两个不重合的二次函数图象关于![]() 轴对称,则称这两个二次函数为“关于
轴对称,则称这两个二次函数为“关于![]() 轴对称的二次函数”.
轴对称的二次函数”.
(1)请写出两个“关于![]() 轴对称的二次函数”;
轴对称的二次函数”;
(2)已知两个二次函数![]() 和
和![]() 是“关于
是“关于![]() 轴对称的二次函数”,求函数
轴对称的二次函数”,求函数![]() 的顶点坐标(用含
的顶点坐标(用含![]() 的式子表示).
的式子表示).
科目:初中数学 来源: 题型:
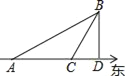
【题目】如图,某船于上午11时30分在A处观察海岛B在北偏东60°,该船以10海里/小时的速度向东航行至C处,再观察海岛在北偏东30°,且船距离海岛20海里.
(1)求该船到达C处的时刻.
(2)若该船从C处继续向东航行,何时到达B岛正南的D处?
查看答案和解析>>
科目:初中数学 来源: 题型:
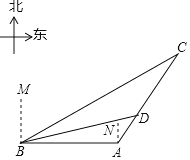
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
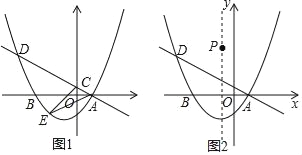
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
(1)求抛物线的函数表达式;
(2)当点D在第二象限且满足CD=5AC时,求直线l的解析式;
(3)在(2)的条件下,点E为直线l下方抛物线上的一点,直接写出△ACE面积的最大值;
(4)如图2,在抛物线的对称轴上有一点P,其纵坐标为4,点Q在抛物线上,当直线l与y轴的交点C位于y轴负半轴时,是否存在以点A,D,P,Q为顶点的平行四边形?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
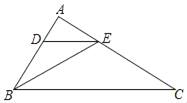
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,AE2=ADAB,∠ABE=∠ACB.
(1)求证:DE∥BC;
(2)如果S△ADE:S四边形DBCE=1:8,求S△ADE:S△BDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“国家卫生城市”,进一步优化市中心城区的环境,德州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造,根据市政建设的需要,须在60天内完成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程的时间比甲队单独完成多用25天,甲、乙两队合作完成工程需要30天,甲队每天的工程费用2500元,乙队每天的工程费用2000元.
(1)甲、乙两个工程队单独完成各需多少天?
(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
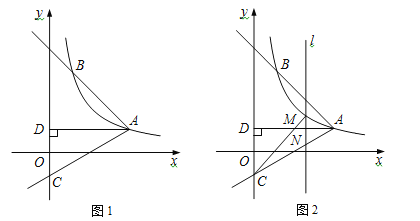
【题目】如图1,反比例函数![]() (x>0)的图象经过点A(
(x>0)的图象经过点A(![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com