
����Ŀ�����꣬�ҹ��������������������������Υ���ж���������������������ڹ���֮�⣮��ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60���������150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�������ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75![]() ���
���
��1����B�㵽ֱ��CA�ľ��룻
��2��ִ������A��D�����˶��ٺ��������������ţ�
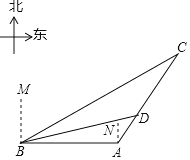
���𰸡�ִ������A��D�����ˣ�75��25![]() �����
�����
�������������������1������B��BH��CA��CA���ӳ����ڵ�H������֪�ɵá�BCA =30����
����30��������ֱ�DZߵ���б�ߵ�һ�뼴�����BH�ij�����B�㵽ֱ��CA�ľ��룻
��2����BD��BH�ij����ù��ɶ����ɵ�DH�ij�����Rt��ABH�У�����tan��BAH=![]() ���AH�ij����Ӷ��ɵ�AD�ij�.
���AH�ij����Ӷ��ɵ�AD�ij�.
�����������1������B��BH��CA��CA���ӳ����ڵ�H��
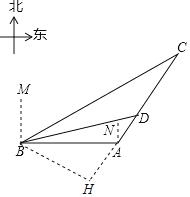
�ߡ�MBC=60�㣬
���CBA=30�㣬
�ߡ�NAD=30�㣬
���BAC=120�㣬
���BCA=180�㩁��BAC����CBA=30�㣬
��BH=BC��sin��BCA=150��![]() =75�������
=75�������
��B�㵽ֱ��CA�ľ�����75���
��2����BD=75![]() ���BH=75���
���BH=75���
��DH=![]() =75�������
=75�������
�ߡ�BAH=180�㩁��BAC=60�㣬
��Rt��ABH��tan��BAH=![]() =
=![]() ��
��
��AH=25![]() ��
��
��AD=DH��AH=��75��25![]() ���������
���������
��ִ������A��D�����ˣ�75��25![]() �����
�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬�ı���OABC�Ǿ��Σ�OA��x��ĸ������ϣ�OC��y����������ϣ�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת
��ͼ1��������OABC�Ƶ�O˳ʱ�뷽����ת![]() �õ�����
�õ�����![]() ������A�Ķ�Ӧ��
������A�Ķ�Ӧ��![]() ����BC����ʱ�����
����BC����ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��ͼ��������OABC�Ƶ�O˳ʱ�뷽����
��ͼ��������OABC�Ƶ�O˳ʱ�뷽����![]() �õ�����
�õ�����![]() ������B�Ķ�Ӧ��
������B�Ķ�Ӧ��![]() ���������������ʱ�����
���������������ʱ�����![]() �����ꣻ
�����ꣻ
![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ3�����
����ͼ3�����![]() ��BC���ڵ�E����
��BC���ڵ�E����![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ��Ķ����ڵ�һ���ޣ��ҹ��㣨0��1���ͣ���1��0�������н��ۣ���ab��0����b2��4����0��a+b+c��2����0��b��1���ݵ�x����1ʱ��y��0��������ȷ���۵ĸ����ǣ�������
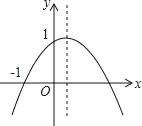
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
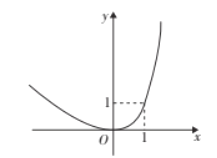
����Ŀ������ijһ�����������¶��壺������ʵ��p�������Ա�����ֵΪpʱ���亯��ֵ����p,���pΪ��������IJ���ֵ.�ں������ڲ���ֵʱ,�ú��������ֵ����С����ֵ֮��q��Ϊ��������IJ��䳤��.�ر��,������ֻ��һ������ֵʱ,�䲻�䳤��qΪ��.���磺��ͼ�еĺ�����0,1��������ֵ,�䲻�䳤��q����1.
(1)�ֱ��жϺ���y=x-1��y=x-1,y=x2��û�в���ֵ������У�ֱ��д���䲻�䳤�ȣ�
(2)����y=2x2-bx.
�����䲻�䳤��Ϊ�㣬��b��ֵ��
����1��b��3,���䲻�䳤��q��ȡֵ��Χ��
(3) �Ǻ���y=x2-2x(x��m)��ͼ��ΪG1����G1��x=m���ۺ�õ��ĺ���ͼ���ΪG2������G��ͼ����G1��G2��������ɣ����䲻�䳤��q����0��q��3,��m��ȡֵ��ΧΪ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
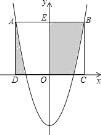
����Ŀ����֪���κ���y=2x2+m����1�����㣨-2��y1���루3��y2���ڴ˶��κ�����ͼ���ϣ���y1_________y2��������������=����������������2����ͼ���˶��κ�����ͼ���㣨0��-4����������ABCD�Ķ���C��D��x���ϣ�A��Bǡ���ڶ��κ�����ͼ���ϣ���ͼ����Ӱ���ֵ����֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ���ֱ��Ϊ1������O������BAD��90�㣬BC��a���ף�CD��b���ף������н�����ȷ����(����)
��sin��BAC��a����cos��BAC��b����tan��BAC��![]() ��
��
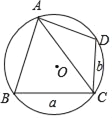
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
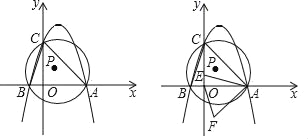
����Ŀ����ͼ��������y����(x+1)(x��3)��x��ֱ��ڵ�A��B(��A��B���Ҳ�)����y�ύ�ڵ�C����P�ǡ�ABC�����Բ��
(1)ֱ��д����A��B��C�����꼰�����ߵĶԳ��
(2)����P�İ뾶��
(3)��D�������ߵĶԳ����ϣ��ҡ�BDC��90�㣬���D�������ȡֵ��Χ��
(4)E���߶�CO�ϵ�һ�����㣬���߶�AE�Ƶ�A��ʱ����ת45����߶�AF�����߶�OF����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������غϵĶ��κ���ͼ�����![]() ��Գƣ�������������κ���Ϊ������
��Գƣ�������������κ���Ϊ������![]() ��ԳƵĶ��κ�����.
��ԳƵĶ��κ�����.
��1����д������������![]() ��ԳƵĶ��κ�������
��ԳƵĶ��κ�������
��2����֪�������κ���![]() ��
��![]() �ǡ�����
�ǡ�����![]() ��ԳƵĶ��κ�����������
��ԳƵĶ��κ�����������![]() �Ķ������꣨�ú�
�Ķ������꣨�ú�![]() ��ʽ�ӱ�ʾ��.
��ʽ�ӱ�ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��a��0������B��2��a��0������A��B����ߣ���C��1����1��������AC��BC������AB��BC��AC��Χ�������ڣ����߽磩��������������궼Ϊ�����ĵ�ĸ���Ϊ4������ôa��ȡֵ��ΧΪ������
A. ��1��a��0B. 0��a��1C. ��1��a��1D. ��2��a��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com