
����Ŀ���������ͼ�ѧУΪ�˵����ص�ѧ�ƽ����ʦ���䱸����ѧУ������ĸ���ͳ�ص�ѧ�ƿ�չѧ����ϲ����ѧ�Ƶ����ʾ����ÿ��ѧ����ѡ��ֻѡһ�����ͼ����ij��ѧ��������ݻ��Ƴ�������������ͳ��ͼ������������⣺ 
��1������뱾�ε���Ĺ��ж�����ѧ��������ȫ����ͳ��ͼ��
��2��������ͳ��ͼ�У���ϲ������«�ӻ�������Ӧ�����ε�Բ�ĽǵĶ�����
��3������������Լ��12000����ѧ��������ϲ�������ա��Ĺ��ж�����ѧ����
���𰸡�
��1���⣺���뱾�ε��������Ϊ��100��20%=500���ˣ���
ϲ������«�ӻ���������Ϊ��500��100��220��80=100���ˣ���
����ͳ��ͼ��ͼ��ʾ��
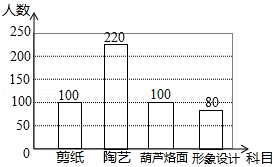
��2���⣺������ͳ��ͼ�У�ϲ������«�ӻ���������ռ�����������İٷֱ�Ϊ��100��500=20%��
�ʡ�ϲ������«�ӻ�������Ӧ�����ε�Բ�ĽǵĶ���Ϊ��20%��360��=72�㣻
��3���⣺ϲ�������ա���ѧ��ռ�ı���Ϊ��220��500=44%��
�ʵ�����ϲ�������ա�������Լ�У�12000��44%=5280���ˣ���
����������1��������ͼ��֪ϲ����ֽ����100�ˣ���������ͼ��֪ϲ����ֽ��ռ�����20%���Ӷ���������뱾�ε������������2���ȸ�������ͼ�����ϲ������«�ӻ���������ռ�����������İٷֱȣ��ٳ���360���������ռ��Բ�ĽǶ�������3�������ϲ�������ա���ѧ���İٷֱȣ��ٳ���12000�Ϳ��Թ��Ƶ�����ϲ�������ա���������
�����㾫�����������⣬������Ҫ�˽�����ͳ��ͼ(������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯���)����Ҫ��������ͳ��ͼ(������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪ���κ���y=ax2+bx+c��ͼ��������˵���У� ��ac��0��
�ڷ���ax2+bx+c=0�ĸ���x1=��1��x2=3��
��a+b+c��0��
�ܵ�x��1ʱ��y����x�����������
��ȷ��˵���� �� ����д��������ȷ����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�MΪBC����һ�㣬����AM������D��DE��AM������ΪE����DE=DC=1��AE=2EM����BM�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��BD��EF��AE��BD���ڵ�C������ABC=30�㣬��BAC=75�㣬���CEF�Ĵ�СΪ�� �� 
A.60��
B.75��
C.90��
D.105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BD��CE�ֱ�ΪAC��AB���ϵ����ߣ�BD��CE����BD=4��CE=6�����ABC�����Ϊ�� ��
A.12
B.24
C.16
D.32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λ�˶�Ա��һ��2000�׳��ı�ֱ��·�Ͻ����ܲ�������������ʼʱ������㣬���ڼ�ǰ��200�ף�����ͬʱͬ���������ǰ�������ٶ���8��/�룬�ҵ��ٶ���6��/�룬�ȵ��յ������յ�ԭ�صȴ�����ס�������֮��ľ�����y�ף�����ʱ����x�룬�����˶������յ��ʱ����������������y��x֮��ĺ���ͼ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ���DAC�͡�DBE���ǵȱ������Σ� 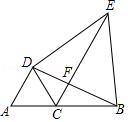
��1����֤����DAB�ա�DCE��
��2��BD��CE���ڵ�F������ADBΪ�۽ǣ��ڲ������κθ����ߵ�����£�ֱ��д��ͼ�����в���60������ȵ���ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ŷֱ����������Ρ�ƽ���ı��Ρ�����ͼ���Ŀ�Ƭ�����dz�ͼ������ȫ��ͬ���ѿ�Ƭ���泯��ϴ�ȣ����������ȡһ�ź�Żأ��ٱ��泯��ϴ�ȣ����������ȡһ�ţ������γ����ÿһ�ſ�Ƭ��ͼ��������Գ�ͼ���������ĶԳ�ͼ�εĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y1=kx+b��ͼ���뷴��������y2= ![]() ��ͼ���ڵ�A����4��m��������y�ύ�ڵ�B����һ�����ڵ�C�ڷ���������y2=
��ͼ���ڵ�A����4��m��������y�ύ�ڵ�B����һ�����ڵ�C�ڷ���������y2= ![]() ��ͼ���ϣ����Ե�CΪԲ�ĵ�Բ��x�ᣬy��ֱ������ڵ�D��B
��ͼ���ϣ����Ե�CΪԲ�ĵ�Բ��x�ᣬy��ֱ������ڵ�D��B 
��1����m��ֵ��
��2����һ�κ����ı���ʽ��
��3������ͼ��y1��y2��0ʱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com