
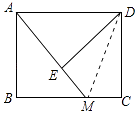
【题目】如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为 . 
【答案】![]()
【解析】解:∵四边形ABCD是矩形, ∴AB=DC=1,∠B=∠C=90°,AD∥BC,AD=BC,
∴∠AMB=∠DAE,
∵DE=DC,
∴AB=DE,
∵DE⊥AM,
∴∠DEA=∠DEM=90°,
在△ABM和△DEA中,  ,
,
∴△ABM≌△DEA(AAS),
∴AM=AD,
∵AE=2EM,
∴BC=AD=3EM,
连接DM,如图所示:
在Rt△DEM和Rt△DCM中, ![]() ,
,
∴Rt△DEM≌Rt△DCM(HL),
∴EM=CM,
∴BC=3CM,
设EM=CM=x,则BM=2x,AM=BC=3x,
在Rt△ABM中,由勾股定理得:12+(2x)2=(3x)2 ,
解得:x= ![]() ,
,
∴BM= ![]() ;
;
故答案为: ![]() .
.
由AAS证明△ABM≌△DEA,得出AM=AD,证出BC=AD=3EM,连接DM,由HL证明Rt△DEM≌Rt△DCM,得出EM=CM,因此BC=3CM,设EM=CM=x,则BM=2x,AM=BC=3x,在Rt△ABM中,由勾股定理得出方程,解方程即可.


科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
(1)求△ABC的面积;
(2)景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ![]() ;
;
其中正确的是(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹); 
(2)如图2,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= ![]() CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用:
CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用: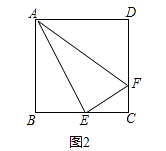
(3)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时点P的坐标. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的弦,点C是 ![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD; 
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是 ![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°; 
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO= ![]() ,求
,求 ![]() 的值.
的值. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC. 
(1)求证:直线BF是⊙O的切线.
(2)若CD=2 ![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】道外区劳技学校为了调整重点学科建设和师资配备,对学校开设的四个传统重点学科开展学生较喜爱的学科调查问卷活动(每名学生必选且只选一项).如图是在某中学调查的数据绘制成两幅不完整的统计图,解答下列问题: 
(1)求参与本次调查的共有多少名学生?并补全条形统计图.
(2)在扇形统计图中,求喜爱“葫芦烙画”所对应的扇形的圆心角的度数?
(3)若道外区大约有12000名中学生,估计喜欢“陶艺”的共有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某微店销售甲、乙两种商品,卖出6件甲商品和4件乙商品可获利120元;卖出10件甲商品和6件乙商品可获利190元.
(1)甲、乙两种商品每件可获利多少元?
(2)若该微店甲、乙两种商品预计再次进货200件,全部卖完后总获利不低于2300元,已知甲商品的数量不少于120件.请你帮忙设计一个进货方案,使总
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com