
【题目】如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
(1)求△ABC的面积;
(2)景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ![]() ≈1.414).
≈1.414).
【答案】
(1)
解:作CE⊥BA于E.
在Rt△AEC中,∠CAE=180°﹣60.7°﹣66.1°=53.2°,
∴CE=ACsin53.2°≈1000×0.8=800米.
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×1400×800=560000平方米.
×1400×800=560000平方米.
(2)
解:连接AD,作DF⊥AB于F.,则DF∥CE.
∵BD=CD,DF∥CE,
∴BF=EF,
∴DF= ![]() CE=400米,
CE=400米,
∵AE=ACcos53.2°≈600米,
∴BE=AB+AE=2000米,
∴AF= ![]() EB﹣AE=400米,
EB﹣AE=400米,
在Rt△ADF中,AD= ![]() =400
=400 ![]() =565.6米.
=565.6米.
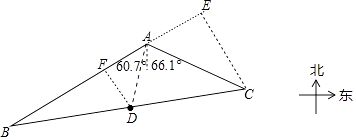
【解析】(1)作CE⊥BA于E.在Rt△ACE中,求出CE即可解决问题;(2)接AD,作DF⊥AB于F,则DF∥CE.首先求出DF、AF,再在Rt△ADF中求出AD即可;
【考点精析】根据题目的已知条件,利用关于方向角问题的相关知识可以得到问题的答案,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】抛物线y1=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. 
(1)求这条抛物线的表达式;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,若点C在直线y2=﹣3x+t上,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD. 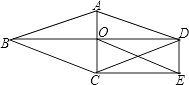
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中: ①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
“文明在我身边”摄影比赛成绩统计表
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x≤100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题:
(1)统计表中c的值为;样本成绩的中位数落在分数段中;
(2)补全频数分布直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评作品数量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( ) 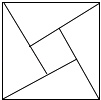
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为 ![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000). 
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2 , 栽花部分的面积不少于100m2 , 请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,△DAC和△DBE都是等边三角形. 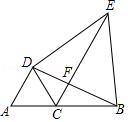
(1)求证:△DAB≌△DCE;
(2)BD、CE交于点F,若∠ADB为钝角,在不添加任何辅助线的情况下,直接写出图中所有不是60°且相等的锐角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com