
【题目】抛物线y1=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. 
(1)求这条抛物线的表达式;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,若点C在直线y2=﹣3x+t上,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求n的取值范围.
【答案】
(1)解:∵抛物线与y轴交于点C,
∴C(0,﹣3).
∵抛物线与x轴交于A、B两点,OB=OC,
∴B(3,0)或B(﹣3,0).
∵点A在点B的左侧,m>0,
∴抛物线经过点B(3,0).
∴0=9m+3(m﹣3)﹣3.
∴m=1.
∴抛物线的表达式为y1=x2﹣2x﹣3
(2)解:由(1)可知:y1=x2﹣2x﹣3=(x﹣1)2﹣4,
∵点C在直线y2=﹣3x+t上,
∴t=﹣3,
∴y2=﹣3x﹣3,
y1向左平移n个单位后,则表达式为:y3=(x﹣1+n)2﹣4,
则当x≥1﹣n时,y随x增大而增大,
y2向下平移n个单位后,则表达式为:y4=﹣3x﹣3﹣n,
要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4,
即(1﹣n﹣1+n)2﹣4≤﹣3(1﹣n)﹣3﹣n,
解得:n≥1
【解析】(1)由抛物线的解析式易求点C的坐标,进而可求出点B的坐标,把点B的坐标代入抛物线的解析式可求出m的值,则抛物线的解析式也可求出;(2)由点C在直线y2=﹣3x+t上,可知t=﹣3,若y1向左平移n个单位后,则表达式为:y3=(x﹣1+n)2﹣4,若y2向下平移n个单位后,则表达式为:y4=﹣3x﹣3﹣n,要使平移后直线与P有公共点,则当x=1﹣n,y3≤y4 , 进而可求出n的取值范围.
【考点精析】根据题目的已知条件,利用二次函数图象的平移和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为6cm , 7.5cm , 9cm , △DEF的一边长为4cm , 当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°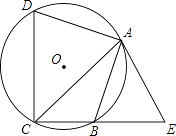
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.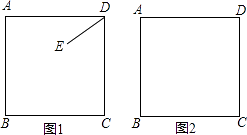
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
(1)求△ABC的面积;
(2)景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ![]() ≈1.414).
≈1.414).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com