
【题目】应我市创建文明城市要求,某小区业主委员会决定把一块长![]() ,宽
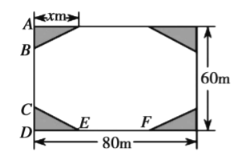
,宽![]() 的矩形空地建成,花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度-样,其宽度不小于
的矩形空地建成,花园小广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的直角三角形),空白区域为活动区,且四周出口宽度-样,其宽度不小于![]() ,不大于
,不大于![]() ,预计活动区造价
,预计活动区造价![]() ,绿化区造价
,绿化区造价![]() ,设绿化区较长直角边为
,设绿化区较长直角边为![]() .
.
(1)求工程队总造价![]() (元)与
(元)与![]() 的函数关系式,并求出x的取值范围;
的函数关系式,并求出x的取值范围;
(2)如果业主委员会最多投资![]() 万元,能否完成全部工程?若能,请写出
万元,能否完成全部工程?若能,请写出![]() 为整数的所有工程方案;若不能,请说明理由.
为整数的所有工程方案;若不能,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )

A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在线段BA上以每秒3cm的速度点A运动,同时动点N从点C出发,在线段CB上以每秒2cm的速度向点B运动,其中一点到达终点后,另一点也停止运动.运动时间为t秒,连接MN.
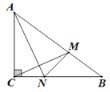
(1)填空:BM= cm.BN= cm.(用含t的代数式表示)
(2)若△BMN与△ABC相似,求t的值;
(3)连接AN,CM,若AN⊥CM,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
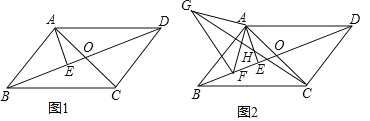
【题目】如图①,在平行四边形ABCD中,对角线AC、BD交于点O,AB=AC,AB⊥AC,过点A作AE⊥BD于点E.
(1)若BC=6![]() ,求AE的长度;
,求AE的长度;
(2)如图②,点F是BD上一点,连接AF,过点A作AG⊥AF,且AG=AF,连接GC交AE于点H,证明:GH=CH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
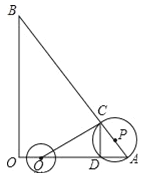
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
(3)若⊙P与线段QC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
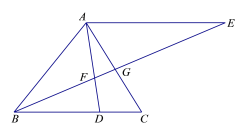
【题目】已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G, ![]() .
.
(1)求证:△CAD∽△CBG;
(2)联结DG,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com