
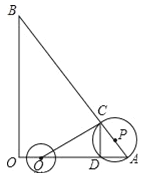
����Ŀ����ͼ������AOB�У���AOBΪֱ�ǣ�OA=6��OB=8���뾶Ϊ2�Ķ�ԲԲ��Q�ӵ�O����������OA������1����λ����/����ٶ������˶���ͬʱ����P�ӵ�A����������AB����Ҳ��1����λ����/����ٶ������˶������˶�ʱ��Ϊt�루0��t��5����PΪԲ�ģ�PA��Ϊ�뾶�ġ�P��AB��OA����һ������ֱ�ΪC��D������CD��QC��
��1����tΪ��ֵʱ����Q���D�غϣ�
��2������Q������Aʱ�����P��OB�صõ��ҳ���
��3������P���߶�QCֻ��һ�������㣬��t��ȡֵ��Χ��
���𰸡���1��![]() ����2��
����2��![]() ����3��0��t��
����3��0��t��![]() ��
��![]() ��t��5��
��t��5��
��������
��1��������֪CD��OA��������ACD�ס�ABO�����ö�Ӧ�ߵı����AD�ij��ȣ���Q��D�غ�ʱ����AD+OQ=OA���г����̼������t��ֵ��
��2������0��t��5����Q����A��ʱ��OQ=4����ʱ��ʱΪ4s������P��PE��OB�ڵ�E�����ô����������������P��OB�صõ��ҳ���
��3������P���߶�QCֻ��һ�������㣬�������������������QC����P����ʱ���������ʱ��ʱ�䣻����Q��D�غ�ʱ���������ʱ��ʱ�䣻����������������ɵó�t��ȡֵ��Χ��
��1����OA=6��OB=8��
���ɹ��ɶ�������ã�AB=10��
������֪��OQ=AP=t��
��AC=2t��
��AC����P��ֱ����
���CDA=90�㣬
��CD��OB��
���ACD�ס�ABO��
��![]() ��
��
��AD=![]() ��
��
��Q��D�غ�ʱ��
AD+OQ=OA��
��![]() +t=6��
+t=6��
��t=![]() ��
��
��2������Q����A��ʱ����ͼ

OQ=OA��QA=4��
��t=![]() =4s��
=4s��
��PA=4��
��BP=AB��PA=6��
����P��PE��OB�ڵ�E����P��OB�ཻ�ڵ�F��G��
����PF��
��PE��OA��
���PEB�ס�AOB��
��![]() ��
��
��PE=3.6��
���ɹ��ɶ�������ã�EF=![]() ��
��
�ɴ�����������֪��FG=2EF=![]() ��
��
��3����QC����P����ʱ����ͼ

��ʱ��QCA=90�㣬
��OQ=AP=t��
��AQ=6��t��AC=2t��
�ߡ�A=��A��
��QCA=��ABO��
���AQC�ס�ABO��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
����0��t��![]() ʱ����P��QCֻ��һ�����㣬
ʱ����P��QCֻ��һ�����㣬
��QC��OAʱ��
��ʱQ��D�غϣ�
�ɣ�1����֪��t=![]() ��
��
����![]() ��t��5ʱ����P��QCֻ��һ�����㣬
��t��5ʱ����P��QCֻ��һ�����㣬
����������������P��QCֻ��һ�����㣬t��ȡֵ��ΧΪ��0��t��![]() ��
��![]() ��t��5��
��t��5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У�PΪBC��һ�㣬DΪAC��һ�㣬�ҡ�APD��60����BP��2��CD��1������ABC�ı߳�Ϊ��������
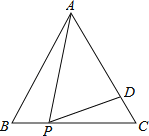
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ǻ�����,������������,���ҳ�֮Ϊ������������ɡ���ѧ����һ�ܿ����������������¼�����,������Щ�ٻ����ջ�,д���Լ�������ʵ��,ƪ���ɳ��ɶ�,��Ҫ�����û��۵ij�����Ծ����,���ڼ�����,ѡ������ƪĿ�ڰ����ʶ���չ��������,����������ѧ�IJ���,�ֶ�����ѧ����д������,ͬʱ��������ѧ���Ĺ۲�������˼ά�����ȵ�,�ﵽ��һʯ��������Ч���� ��ͼ����������ͬ���������һ��Բ�����һ������ͼ�Σ�������ͼ�ǣ� ��
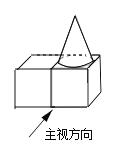
A. B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
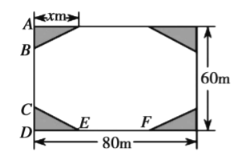
����Ŀ��Ӧ���д�����������Ҫ��,ijС��ҵ��ίԱ�������һ�鳤![]() ,��
,��![]() �ľ��οյؽ��ɣ���С�㳡,��Ʒ�����ͼ��ʾ,��Ӱ����Ϊ�̻���(�Ŀ��̻���Ϊȫ�ȵ�ֱ��������),�հ�����Ϊ���,�����ܳ��ڿ���-��,����Ȳ�С��
�ľ��οյؽ��ɣ���С�㳡,��Ʒ�����ͼ��ʾ,��Ӱ����Ϊ�̻���(�Ŀ��̻���Ϊȫ�ȵ�ֱ��������),�հ�����Ϊ���,�����ܳ��ڿ���-��,����Ȳ�С��![]() ,������
,������![]() ,Ԥ�ƻ�����
,Ԥ�ƻ�����![]() ,�̻������
,�̻������![]() ,���̻����ϳ�ֱ�DZ�Ϊ
,���̻����ϳ�ֱ�DZ�Ϊ![]() .
.
(1)�̶������![]() (Ԫ)��
(Ԫ)��![]() �ĺ�����ϵʽ,�����x��ȡֵ��Χ;
�ĺ�����ϵʽ,�����x��ȡֵ��Χ;
(2)���ҵ��ίԱ�����Ͷ��![]() ��Ԫ,�ܷ����ȫ������?���ܣ���д��
��Ԫ,�ܷ����ȫ������?���ܣ���д��![]() Ϊ���������й��̷���;������,��˵������.
Ϊ���������й��̷���;������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�����Ӽס�������ͬѧ��ѡ��һ�˲μӡ��ж����䡱����������ͬ�IJ��������£��ס�������5�β��Գɼ�����λ���֣����£�
�ף�79��86��82��85��83.
�ң�88��81��85��81��80.
��ش��������⣺
��1���׳ɼ�����λ����______���ҳɼ���������______��
��2��������֪![]() ��
��![]() .��������ķ������ƽ�����ͷ���ĽǶ��Ƽ��μӱ����ĺ�����ѡ.
.��������ķ������ƽ�����ͷ���ĽǶ��Ƽ��μӱ����ĺ�����ѡ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+3������A����1��0����B��3��0������y�ύ�ڵ�C����D��xD��yD��Ϊ��������һ�����㣬����1��xD��3������AC��BC��DB��DC��
��1����������ߵĽ���ʽ��
��2������BCD�����������AOC�������2��ʱ�����D�����ꣻ
��3���ڣ�2���������£�����M��x����һ���㣬��N����������һ���㣬���ж��Ƿ���������ĵ�M��ʹ���Ե�B��D��M��NΪ������ı�����ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ�ǡ�ABC�У�CA=CB����EΪ��ABC��һ�㣬CE=CA����CDƽ�֡�ACB��AE��D���ҡ�CDE=60�㣮
��1����֤����CBEΪ�ȱ������Σ�
��2����AD=5��DE=7����CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ��С����С��������ѧ����ѧ֪ʶ��������ǰС�ӵĿ�������ʱ������ѡ���˺Ӷ��ߵ�һ�ô���������ײ���Ϊ��A�����������ڵİ���ѡ���˵�B��ʹ��AB��Ӱ���ֱ������B��������BC������AB���ӳ�����ѡ���D������DE��ʹ�õ�E���C��A���ߣ�
��֪��CB��AD��ED��AD�����BC��1m��DE��1.5m��BD��8.5m������ʾ��ͼ��ͼ��ʾ���������ز�����Ϣ����ӿ�AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��D��������y��![]() ��x+1��2��5�����㣬�����ߵĶ���ΪE��CD��x�ᣬ�ı���ABCDΪ�����Σ�AB�߾�����E����������ABCD�ı߳�Ϊ_____��
��x+1��2��5�����㣬�����ߵĶ���ΪE��CD��x�ᣬ�ı���ABCDΪ�����Σ�AB�߾�����E����������ABCD�ı߳�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com