练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，直线与轴、轴分别相交于.点的坐标为，点是线段上的一点.

    （1）求的值；（2）若的面积为2，求点的坐标.

    【答案】（1）k= （2）（-，1）

    【解析】

    (1)将点E的坐标代入一次函数解析式中,即可得出关于k的一元一次方程,解方程即可得出结论;

    (2)结合(1)中得k值可得出一次函数解析式,由点E的坐标可得出线段OE的长度,根据三角形的面积公式可求出点P的纵坐标,将点P的纵坐标代入一次函数解析式中即可求出点P的横坐标,由此即可得出结论

    (1)将点E(-4,0)代入到y=kx+3中,

    得:0=-4k+3=0,

    解得:k=

    (2)∵k=

    ∴直线EF的解析式为

    ∵点E的坐标为(-4,0),

    ∴OE=4

    ∴△OPE= OP

    ∴=1

    令中y=1,则,

    解得:x=-

    故当△OPB的面积为2时,点P的坐标为（-，1）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明随机调查了若干市民租用公共自行车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如下统计图。请根据图中信息，解答下列问题：

    [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922393511583744/1923977001213952/STEM/d5900c7cb9b84a9a89aefef7d82bcf93.png]

    （1）这次被调查的总人数是多少？

    （2）试求表示A组的扇形圆心角的度数，并补全条形统计图；

    （3）如果骑自行车的平均速度为12km/h，请估算，在租用公共自行车的市民中，骑车路程不超过6km的人数所占的百分比。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】代数式：①-x；②x2+x-1；③；④；⑤；⑥πm3y；⑦；⑧．

    （1）请上述代数式的序号分别填在相应的圆圈内：

    （2）其中次数最高的多项式是__________次_________项式；

    （3）其中次数最高的单项式的次数是____________，系数是____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，矩形OABC的邻边OA、OC分别与x、y轴重合，矩形OABC的对称中心P(4，3)，点Q由O向A以每秒1个单位速度运动，点M由C向B以每秒2个单位速度运动，点N由B向C以每秒2个单位速度运动，设运动时间为t秒，三点同时出发，当一点到达终点时同时停止.

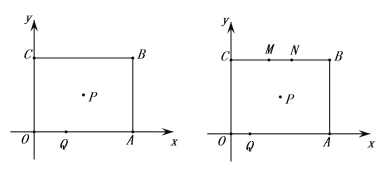
    （1）根据题意，可得点B坐标为__________，AC＝_________；

    （2）求点Q运动几秒时，△PCQ周长最小?

    （3）在点M、N、Q的运动过程中，能否使以点O、Q、M、N为顶点的四边形是平行四边形？若能，请求出t值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，正方形ABCD中，点E、F、G分别是边AD、AB、BC的中点，连接EP、FG．

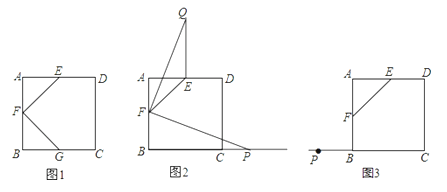
    （1）如图1，直接写出EF与FG的关系____________；

    （2）如图2，若点P为BC延长线上一动点，连接FP，将线段FP以点F为旋转中心，逆时针旋转90°，得到线段FH，连接EH．

    ①求证：△FFE≌△PFG；②直接写出EF、EH、BP三者之间的关系；

    （3）如图3，若点P为CB延长线上的一动点，连接FP，按照(2)中的做法，在图(3)中补全图形，并直接写出EF、EH、BP三者之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，y=x的图象向右平移1个单位得到y=x﹣1的图象，类似的，y=（k≠0）的图象向左平移2个单位得到y=（k≠0）的图象．请运用这一知识解决问题．

    如图，已知反比例函数y=的图象C与正比例函数y=ax（a≠0）的图象l相交于点A（1，m）和点B．

    （1）写出点B的坐标，并求a的值；

    （2）将函数y=的图象和直线AB同时向右平移n（n＞0）个单位长度，得到的图象分别记为C1和l1，已知图象C1经过点M（3，2）．

    ①分别写出平移后的两个图象C1和l1对应的函数关系式；

    ②直接写出不等式+4≤ax的解集．

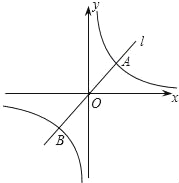
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上有A，B，C三点，分别代表﹣36，﹣10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒．

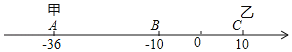
    （1）问多少秒后，甲到A，B，C的距离和为60个单位？

    （2）若乙的速度为6个单位/秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？

    （3）在（1）（2）的条件下，当甲到A、B、C的距离和为60个单位时，甲调头返回．问甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

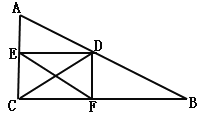
    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=2，BC=4，点D为边AB上一动点，DE⊥AC，DF⊥BC，垂足为E，F. 连接EF，CD.

    （1）求证：EF＝CD；

    （2）当EF为何值时，EF∥AB；

    （3）当四边形ECFD为正方形时，求EF的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

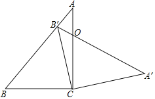
    【题目】如图，△ABC中，∠ACB＝90°,∠B＝50°,△ABC绕点C顺时针旋转得到△A′B′C，点B′恰好落在线段AB上，AC、A′B′相交于O，则∠COA′的度数为_________．

    查看答案和解析>>

    同步练习册答案