
【题目】已知数轴上有A,B,C三点,分别代表﹣36,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒.
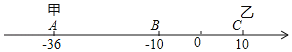
(1)问多少秒后,甲到A,B,C的距离和为60个单位?
(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,问甲,乙在数轴上的哪个点相遇?
(3)在(1)(2)的条件下,当甲到A、B、C的距离和为60个单位时,甲调头返回.问甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
【答案】(1)经过3s或10s后,甲到A,B,C的距离和为60个单位;(2)甲,乙在数轴上的点﹣17.6相遇;(3)甲从A向右运动3秒时返回,能在数轴上与乙相遇,相遇点表示的数为﹣56.
【解析】
(1)设x秒后甲到A,B,C三点的距离之和为60个单位,分甲应为于AB或BC之间两种情况讨论即可求解;
(2)可设x秒后甲与乙相遇,根据甲与乙的路程和为46,可列出方程求解即可;
(3)设y秒后甲到A,B,C三点的距离之和为60个单位,分甲应为于AB或BC之间两种情况讨论即可求解.
解:(1)设x秒后,甲到A,B,C的距离和为60个单位.
B点距A,C两点的距离为26+20=46<60,
A点距B、C两点的距离为26+46=72>60,
C点距A、B的距离为46+20=66>40,
故甲应位于AB或BC之间.
①AB之间时:4x+(26﹣4x)+(26﹣4x+20)=60,x=3;
②BC之间时:4x+(4x﹣26)+(46﹣4x)=60,x=10,
综上所述,经过3s或10s后,甲到A,B,C的距离和为60个单位;
(2)设ts后甲与乙相遇
4t+6t=46,
解得:x=4.6,
4×4.6=18.4,﹣36+18.4=﹣17.6
答:甲,乙在数轴上的点﹣17.6相遇;
(3)设y秒后甲到A,B,C三点的距离之和为60个单位,
①甲从A向右运动3秒时返回,此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:﹣36+4×3﹣4y;乙表示的数为:10﹣6×3﹣6y,
依据题意得:﹣36+4×3﹣4y=10﹣6×3﹣6y,
解得:y=8,
相遇点表示的数为:﹣36+4×3﹣4y=﹣56(或:10﹣6×3﹣6y=﹣56),
②甲从A向右运动10秒时返回,设y秒后与乙相遇.
甲表示的数为:﹣36+4×10﹣4y;乙表示的数为:10﹣6×10﹣6y,
依据题意得:﹣36+4×10﹣4y=10﹣6×10﹣6y,
解得:y=﹣27(不合题意舍去),
即甲从A向右运动3秒时返回,能在数轴上与乙相遇,相遇点表示的数为﹣56.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
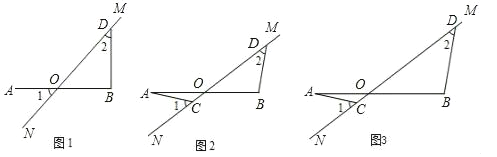
【题目】在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,⊙![]() 与直线
与直线![]() 都相切.不论⊙
都相切.不论⊙![]() 如何转动,直线
如何转动,直线![]() 之间的距离始终保持不变(等于⊙
之间的距离始终保持不变(等于⊙![]() 的半径).我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.
的半径).我们把具有这一特性的图形称为“等宽曲线”.图2是利用圆的这一特性的例子.将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进.据说,古埃及就是利用只有的方法将巨石推到金字塔顶的.

拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”.如图4,夹在平行线![]() 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线
之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变.若直线![]() 之间的距离等于
之间的距离等于![]() ,则莱洛三角形的周长为
,则莱洛三角形的周长为 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次3个数:2、9、7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2、7、9、-2、7,这称为第1次操作,做第2次同样的操作后也可以产生一个新数串:2、5、7、2、9、-11、-2、9、7,继续依次操作下去,问从数串2、9、7开始操作第20次后所产生的那个数串的所有数之和是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD的外侧作等腰△ABE,AE=BE,连接ED、EC.
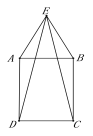
(1)求证:ED=EC.
(2)用无刻度的直尺作出△EDC中DC边上的高EH.(不写作法,保留作图的痕迹)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com