练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD的外侧作等腰△ABE，AE=BE，连接ED、EC．

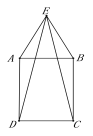
    （1）求证：ED=EC．

    （2）用无刻度的直尺作出△EDC中DC边上的高EH.（不写作法，保留作图的痕迹）

    【答案】(1) ED=EC (2)如图所示

    【解析】

    (1)利用ΔADE≌ΔBCE,AE=BE,∠EAD=∠EBD,AD=BC.全等三角形，对应边相等，所以ED=EC。

    （2）作ED、CE的平行线相较于点F，连接EF，与CD相交于点H，即EH是三角形DC边上的高.

    (1)证明：四边形ABCD是矩形，

    AD=BC，∠DAB=∠CBA

    △ABE是等腰三角形，

    AE=AB，∠EAB=∠EBA.

    ∠DAB+∠EAB=∠CBA+∠EBA

    ∠EAD=∠EBC

    在ΔADE和ΔBCE中

    ΔADE≌ΔBCE(SAS)

    ED=EC

    （2）如图所示

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知数轴上有A，B，C三点，分别代表﹣36，﹣10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒．

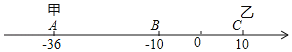
    （1）问多少秒后，甲到A，B，C的距离和为60个单位？

    （2）若乙的速度为6个单位/秒，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，问甲，乙在数轴上的哪个点相遇？

    （3）在（1）（2）的条件下，当甲到A、B、C的距离和为60个单位时，甲调头返回．问甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知ac＞0，a+b＜0，且|c|＞|b|，数轴上a、b、c对应的点是A、B、C．

    （1）若|a|＝a时，请在数轴上标出点A、B、C的大致位置；

    （2）在（1）的条件下，化简：|a+b|+|b+c|﹣|c﹣a|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB＝90°,∠B＝50°,△ABC绕点C顺时针旋转得到△A′B′C，点B′恰好落在线段AB上，AC、A′B′相交于O，则∠COA′的度数为_________．

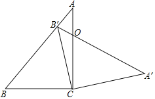
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，∠ABC和∠BCD的平分线交边AD于点E，且BE=12，CE=5，则点AB与CD之间的距离是____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P时直线AC下方抛物线上的动点．

    （1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；

    （3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是按照一定规律画出的“树形图”，经观察可以发现：图A2比图A1多出2个“树枝”，图A3比图A2多出4个“树枝”，图A4比图A3多出8个“树枝”……照此规律，图A6比图A2多出“树枝”( )

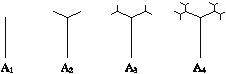
    A.32个B.56个C.60个D.64个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

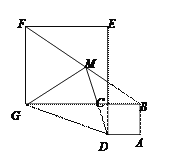
    【题目】如图，正方形ABCD和正方形CEFG的面积分别为4 cm2,36cm2, 点G,C,B在一条直线上，M是BF的中点，则点M到GD的距离为_________cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为响应“书香校园”号召，重庆一中在九年级学生中随机抽取某班学生对2016年全年阅读中外名著的情况进行调查，整理调查结果发现，每名学生阅读中外名著的本数，最少的有5本，最多的有8本，并根据调查结果绘制了如图所示的不完整的折线统计图和扇形统计图.

    （1）该班学生共有 名，扇形统计图中阅读中外名著本数为7本所对应的扇形圆心角的度数是 度，并补全折线统计图；

    （2）根据调查情况，班主任决定在阅读中外名著本数为5本和8本的学生中任选两名学生进行交流，请用树状图或表格求出这两名学生阅读的本数均为8本的概率.

    查看答案和解析>>

    同步练习册答案