
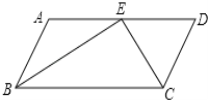
【题目】如图,在□ABCD中,∠ABC和∠BCD的平分线交边AD于点E,且BE=12,CE=5,则点AB与CD之间的距离是____
【答案】![]()
【解析】
根据平行四边形的性质可证明△BEC是直角三角形,利用勾股定理可求出BC的长,利用角平分线的性质以及平行线的性质得出∠ABE=∠AEB,∠DEC=∠DCE,进而利用平行四边形对边相等进而得出答案,最后根据平行四边形的面积求出AB与CD之间的距离.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的角平分线的交点E落在AD边上,
∴∠EBC+∠ECB=![]() ×180°=90°,
×180°=90°,
∴∠BEC=90°,
∵BE=12,CE=5,
∴BC=![]() =13
=13
作EM⊥BC于M,
则EM=![]() =
=![]()
∴点A到BC的距离是![]()
∵AD∥BC, ∠ABC和∠BCD的平分线交边AD于点E,
∴AE=AB,ED=CD,即AB=CD=![]() AD=
AD=![]()
延长CD,过B点作BH⊥CD于H,即BH就是AB到CD的距离。
∵S平行四边形ABCD=EM×BC=13×![]() =
=![]() ;
;
∴S平行四边形ABCD=CD×BH=![]() ×BH=
×BH=![]()
∴BH=![]()


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
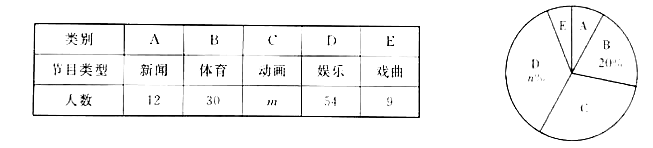
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中![]() 的值为 ,统计图中
的值为 ,统计图中![]() 的值为 ;
的值为 ;
(3)在统计图中,![]() 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列7个数
+4,﹣|﹣2|,-20%,![]() ,0,-(-1),3.14
,0,-(-1),3.14
(1)画出数轴,并将上面的七个数表示在数轴上;
(2)下图的两个圈的交叉部分表示什么数的集合,请填写在横线上,并把七个数中适合的数填写到两个圈的交叉部分.
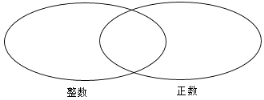
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.
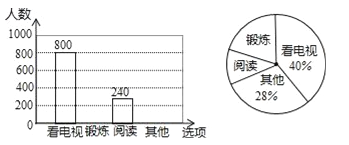
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了 名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
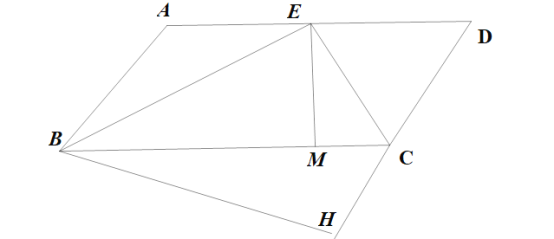
【题目】如图,在矩形ABCD的外侧作等腰△ABE,AE=BE,连接ED、EC.
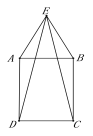
(1)求证:ED=EC.
(2)用无刻度的直尺作出△EDC中DC边上的高EH.(不写作法,保留作图的痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
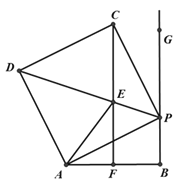
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() (
(![]() )与直线
)与直线![]() 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,点![]() ,
,![]() 表示的数互为相反数,结合数轴回答下列问题:
表示的数互为相反数,结合数轴回答下列问题:
![]()
(1)请在数轴上标出原点![]() 的位置.
的位置.
(2)直接写出点![]() ,
,![]() ,
,![]() ,
,![]() 所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
(3)从A,B两题中任选一题作答.
A. ①若点![]() 在数轴上,与点
在数轴上,与点![]() 的距离
的距离![]() ,求点
,求点![]() 表示的数;
表示的数;
②设动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点
出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
B.设点![]() ,
,![]() 都从点
都从点![]() 出发沿数轴的正方向匀速向终点
出发沿数轴的正方向匀速向终点![]() 运动.点
运动.点![]() 的速度为每秒2个单位长度,点
的速度为每秒2个单位长度,点![]() 的速度为每秒5个单位长度,当点
的速度为每秒5个单位长度,当点![]() 运动到点
运动到点![]() 时点
时点![]() 开始运动,设点
开始运动,设点![]() 运动的时间为
运动的时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com