
【题目】如图,数轴的单位长度为1,点![]() ,
,![]() 表示的数互为相反数,结合数轴回答下列问题:
表示的数互为相反数,结合数轴回答下列问题:
![]()
(1)请在数轴上标出原点![]() 的位置.
的位置.
(2)直接写出点![]() ,
,![]() ,
,![]() ,
,![]() 所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
(3)从A,B两题中任选一题作答.
A. ①若点![]() 在数轴上,与点
在数轴上,与点![]() 的距离
的距离![]() ,求点
,求点![]() 表示的数;
表示的数;
②设动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点
出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
B.设点![]() ,
,![]() 都从点
都从点![]() 出发沿数轴的正方向匀速向终点
出发沿数轴的正方向匀速向终点![]() 运动.点
运动.点![]() 的速度为每秒2个单位长度,点
的速度为每秒2个单位长度,点![]() 的速度为每秒5个单位长度,当点
的速度为每秒5个单位长度,当点![]() 运动到点
运动到点![]() 时点
时点![]() 开始运动,设点
开始运动,设点![]() 运动的时间为
运动的时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)见解析;(2)![]() ,
,![]() ,
,![]() ,
,![]() ,A点表示的数的平方最大,最大是49;(3)A:① -6.5或0.5;② 当 0<t≤
,A点表示的数的平方最大,最大是49;(3)A:① -6.5或0.5;② 当 0<t≤![]() 时, CP= BC-PB=2-3t;当
时, CP= BC-PB=2-3t;当![]() <t< 2
<t< 2![]() 时,CP=PB-BC= 3t-2;当t ≥2
时,CP=PB-BC= 3t-2;当t ≥2![]() 时,CP=CD=6. ;B:当0<t≤1时,MN=2t;当1<t≤3时,MN=
时,CP=CD=6. ;B:当0<t≤1时,MN=2t;当1<t≤3时,MN=![]() ,当3<t≤5时,MN=10-2t.
,当3<t≤5时,MN=10-2t.
【解析】
(1)根据点![]() ,
,![]() 表示的数互为相反数可以确定为C,D中点,画出即可;
表示的数互为相反数可以确定为C,D中点,画出即可;
(2)根据这些点在数轴上的位置得到A,B,C,D所表示的数,平方最大,即绝对值最大为A.算出平方数即可.
(3)A: ①根据数轴上的位置可以得到F对应的点为两个,分别求出即可;②依据题意列出代数式即可,注意P与C的位置.
B:当0<t≤1时N在A处不动,所以MN距离为M所走距离;
当1<t≤3时M,N都在AD之间,当t=3时,N与D重合,所以MN=![]()
当3<t≤5时,M在AD之间,N在D上,当t=5时,M,N同时在D上,所以MN=10-2t.
解:(1)如图:

(2)![]() ,
,![]() ,
,![]() ,
,![]()
平方最大为A,平方数最大为49
(3) A:①-6.5或0.5;
② 当P点在C点的左侧或C点时,即0<t≤![]() 时, CP= BC-PB=2-3t
时, CP= BC-PB=2-3t
当P点在C点右侧直到到达D点时,即![]() <t< 2
<t< 2![]() 时,CP=PB-BC= 3t-2;
时,CP=PB-BC= 3t-2;
当P点在C点右侧到达D点不动时,即t ≥2![]() 时,CP=CD=6
时,CP=CD=6
B:M所走的时间为t秒,那么N所走的时间为t-1秒
当M运动,N不动时,MN的距离就是M点运动的距离,即0<t≤1时,MN=2t;
当M,N同时在AD之间时,MN的距离两点运动之差,即1<t≤3时,MN=![]() ;
;
当N到达D点,M还在运动时,MN的距离等于AD的距离与M移动的距离之差,即3<t≤5时,MN=10-2t.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上,求M′的坐标;
(3)已知点C(﹣1,3),D(4,3),点N(x,y)和它的“n级关联点”N′都位于线段CD上,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
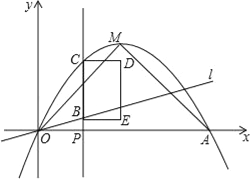
【题目】如图,抛物线y=﹣![]() x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=![]() x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东妈妈准备购买若干个粽子和咸鸭蛋(每个棕子的价格相同,每个咸鸭蛋的价格相同).已知某超市粽子的价格比咸鸭蛋的价格贵1.8元,小东妈妈发现,花30元购买粽子的个数与花12元购买的咸鸭蛋个数相同.
(1)求该超市粽子与咸鸭蛋的价格各是多少元?
(2)小东妈妈计划购买粽子与咸鸭蛋共18个,她的一张购物卡上还有余额40元,若只用这张购物卡,她最多能购买粽子多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香校园”号召,重庆一中在九年级学生中随机抽取某班学生对2016年全年阅读中外名著的情况进行调查,整理调查结果发现,每名学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的折线统计图和扇形统计图.

(1)该班学生共有 名,扇形统计图中阅读中外名著本数为7本所对应的扇形圆心角的度数是 度,并补全折线统计图;
(2)根据调查情况,班主任决定在阅读中外名著本数为5本和8本的学生中任选两名学生进行交流,请用树状图或表格求出这两名学生阅读的本数均为8本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
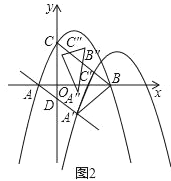
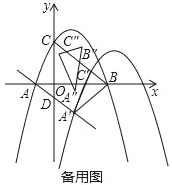
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
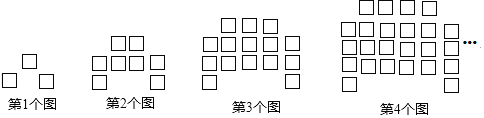
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com