
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
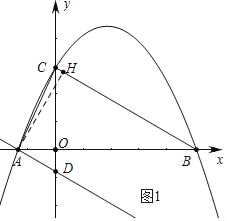
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
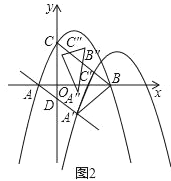
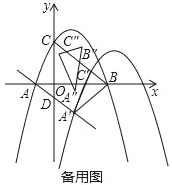
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.

【答案】(1)AD与BC之间的距离为![]() ;(2)点Q经过的最短路径的长为
;(2)点Q经过的最短路径的长为![]() +
+![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)如图1中,作AH⊥BC于H,先求得点A、B、C的坐标,即可得OA、OB、OC的长,根据勾股定理求得BC的长,利用S△ABC=![]() ABCO=
ABCO=![]() BCAH,即可求得AH的长,从而求得平行线AD、BC之间的距离;(2)如图2中,设P(m,﹣
BCAH,即可求得AH的长,从而求得平行线AD、BC之间的距离;(2)如图2中,设P(m,﹣![]() m2+
m2+![]() m+3),由S△PBC=S△POB+S△PCO﹣S△BOC可得S△PBC与m之间的二次函数关系式,根据二次函数的性质求得点P的坐标,作B关于直线AD的对称点B′交AD于K,连接PK交BC于M,作MN⊥AD于N,连接BN,则PM+MN+BN的值最小.求得PM+MN+BN的值即可;(3)如图3中,作DG⊥A′C′于G,AH⊥BC于H,A′K⊥BC于K.分两种情况求DK2的值即可.
m+3),由S△PBC=S△POB+S△PCO﹣S△BOC可得S△PBC与m之间的二次函数关系式,根据二次函数的性质求得点P的坐标,作B关于直线AD的对称点B′交AD于K,连接PK交BC于M,作MN⊥AD于N,连接BN,则PM+MN+BN的值最小.求得PM+MN+BN的值即可;(3)如图3中,作DG⊥A′C′于G,AH⊥BC于H,A′K⊥BC于K.分两种情况求DK2的值即可.
试题解析:
(1)如图1中,作AH⊥BC于H.
对于抛物线y=﹣![]() x2+
x2+![]() x+3,令y=0,得到﹣
x+3,令y=0,得到﹣![]() x2+
x2+![]() x+3=0,解得x=﹣
x+3=0,解得x=﹣![]() 或3
或3![]() ,
,
∴A(﹣![]() ,0),B(3
,0),B(3![]() ,0),
,0),
令x=0,得到y=3,
∴C(0,3),
∴OA=![]() ,OB=3
,OB=3![]() ,AB=4
,AB=4![]() ,OC=3,BC=
,OC=3,BC=![]() =3
=3![]() ,
,
∵S△ABC=![]() ABCO=
ABCO=![]() BCAH,
BCAH,
∴AH=![]() =
=![]() ,
,
∵AD∥BC,
∴AD与BC之间的距离为![]() .
.
(2)如图2中,设P(m,﹣![]() m2+
m2+![]() m+3),
m+3),

S△PBC=S△POB+S△PCO﹣S△BOC
=![]() ×3
×3![]() ×(﹣
×(﹣![]() m2+
m2+![]() m+3)+
m+3)+![]() ×3×m﹣
×3×m﹣![]() ×3
×3![]() ×3
×3
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=![]() 时,△PBC的面积最大,此时P(
时,△PBC的面积最大,此时P(![]() ,
,![]() ),
),
作B关于直线AD的对称点B′交AD于K,连接PK交BC于M,作MN⊥AD于N,连接BN,则PM+MN+BN的值最小.
∵直线BC的解析式为y=﹣![]() x+3,AD∥BC,
x+3,AD∥BC,
∴直线AD的解析式为y=﹣![]() x﹣1,
x﹣1,
∵BB′⊥BC,
∴直线BB′的解析式为y=![]() x﹣6,
x﹣6,
由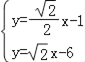 ,解得
,解得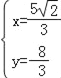 ,
,
∴K(![]() ,﹣
,﹣![]() ),
),
∴直线PK的解析式为y=﹣![]() x+
x+![]() ,
,
由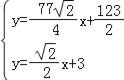 ,解得
,解得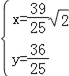 ,
,
∴M(![]()
![]() ,
,![]() ),
),
∴点Q经过的最短路径的长=PM+MN+BN=MN+(PM+MK)=MN+PK,
∵MN=![]() ,PK=
,PK=![]() =
=![]() ,
,
∴点Q经过的最短路径的长为![]() +
+![]() .
.
(3)如图3中,作DG⊥A′C′于G,AH⊥BC于H,A′K⊥BC于K.
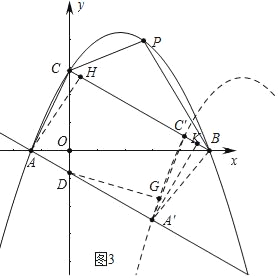
∵A′B=A′C′,AC=A′C′,AA′∥BC,
∴四边形AA′BC是等腰梯形,易知△ACH≌△A′BK,
∴CH=BK=KC′,
由(1)可知,CH=![]() =
=![]() =
=![]() ,
,
∴BC′=![]() ,
,
∴CC′=![]() ,易知C′(
,易知C′(![]()
![]() ,
,![]() ),A′(
),A′(![]()
![]() ,﹣
,﹣![]() ),
),
∴直线A′C′的解析式为y=![]() x﹣
x﹣![]() ,
,
∵DG⊥A′C′,
∴直线DG的解析式为y=﹣![]() x﹣1,
x﹣1,
由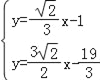 ,解得
,解得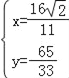 ,
,
∴G(![]() ,﹣
,﹣![]() ),
),
∴DG=![]() ,
,
如图4中,将等腰△A′C′B绕点D逆时针旋转一周的过程中,△DKI是以KI为底边的等腰三角形用图中四种情形,根据对称性可知,DK2的值有两种情形.
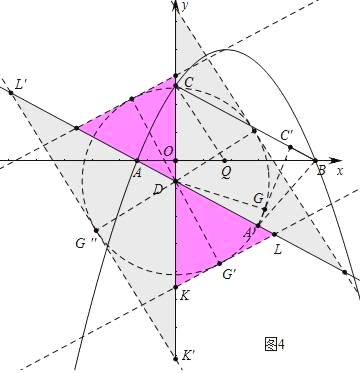
作DG′⊥KL于G′,则DG′=DG=![]() ,作CQ平分∠OCB,
,作CQ平分∠OCB,
∵OC:CB=OQ:QB,BC=![]() =
=![]() =3
=3![]() ,
,
∴OQ:QB=3:3![]() =1:
=1:![]() ,
,
∴OQ=![]() ×3
×3![]() =
=![]() ,
,
在Rt△COQ中,CQ=![]() =
=![]() ,
,
∵DK=DL,DG′⊥KL,
∴∠G′DK=G′DL,
∵BC∥AD,
∴∠G′DK=∠OCQ,∵∠COQ=∠DG′K=90°,
∴△DG′K∽△COQ,
∴![]() =
=![]() ,
,
∴DK2=![]() =
=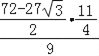 =
=![]() ,
,
同法当△DK′L′是等腰三角形时,作DG″⊥K′L′,易证△DK′G″∽△QCO,
∴![]() =
=![]() ,
,
∴DK′2=![]() =
=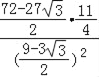 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
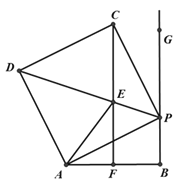
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
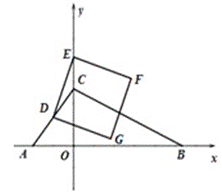
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
(1)求点D的坐标;
(2)记正方形DEFG的面积为S,
① 求S关于n的函数关系式;
② 当DF∥x轴时,求S的值;
(3)是否存在n的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,点![]() ,
,![]() 表示的数互为相反数,结合数轴回答下列问题:
表示的数互为相反数,结合数轴回答下列问题:
![]()
(1)请在数轴上标出原点![]() 的位置.
的位置.
(2)直接写出点![]() ,
,![]() ,
,![]() ,
,![]() 所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
(3)从A,B两题中任选一题作答.
A. ①若点![]() 在数轴上,与点
在数轴上,与点![]() 的距离
的距离![]() ,求点
,求点![]() 表示的数;
表示的数;
②设动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点
出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
B.设点![]() ,
,![]() 都从点
都从点![]() 出发沿数轴的正方向匀速向终点
出发沿数轴的正方向匀速向终点![]() 运动.点
运动.点![]() 的速度为每秒2个单位长度,点
的速度为每秒2个单位长度,点![]() 的速度为每秒5个单位长度,当点
的速度为每秒5个单位长度,当点![]() 运动到点
运动到点![]() 时点
时点![]() 开始运动,设点
开始运动,设点![]() 运动的时间为
运动的时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
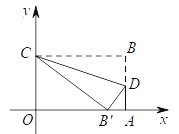
【题目】如图,在平面直角坐标系中,矩形纸片OABC的顶点A,C分别在x轴,y轴的正半轴上,将纸片沿过点C的直线翻折,使点B恰好落在x轴上的点B′处,折痕交AB于点D.若OC=9,![]() ,则折痕CD所在直线的解析式为____.
,则折痕CD所在直线的解析式为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com