
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
(1)求点D的坐标;
(2)记正方形DEFG的面积为S,
① 求S关于n的函数关系式;
② 当DF∥x轴时,求S的值;
(3)是否存在n的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
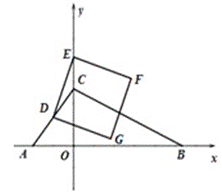
【答案】(1)点D的坐标为(-3,4);(2)①S=(n-4)2+9;②S=(7-4)2+9=18;当n=![]() 或21或3或
或21或3或![]() 时,正方形的顶点F或G落在△ABC的边上.
时,正方形的顶点F或G落在△ABC的边上.
【解析】试题分析:(1)由于点D(m,4)在直线AC上,代入直线AC的解析式可得关于m的方程,解方程即可得到点D的坐标为(﹣3,4);
(2)①如图1,过点D作DH⊥y轴于H,则EH=|n﹣4|,根据正方形的面积公式和勾股定理可得S关于n的函数关系式;
②当DF∥x轴时,点H即为正方形DEFG的中心,可得n=7,再代入函数关系式即可得到S的值;
(3)根据待定系数法可得BC为: ![]() ;再分四种情况:①当点F落在BC边上时;②当点G落在BC边上时;③当点F落在AB边上时;④当点G落在AC边上时;进行讨论可得所有满足条件的n的值.
;再分四种情况:①当点F落在BC边上时;②当点G落在BC边上时;③当点F落在AB边上时;④当点G落在AC边上时;进行讨论可得所有满足条件的n的值.
试题解析:解:(1)∵点D(m,4)在直线AC上;
∴4=![]() m+8,解得m=﹣3,∴点D的坐标为(﹣3,4);
m+8,解得m=﹣3,∴点D的坐标为(﹣3,4);
(2)①如图1,过点D作DH⊥y轴于H,则EH=|n﹣4|
∴S=DE2=EH2+DH2=(n﹣4)2+9;
②当DF∥x轴时,点H即为正方形DEFG的中心,∴EH=DH=3,∴n=4+3=7,∴S=(7﹣4)2+9=18;
(3)∵OB=2OC=16,∴B为(16,0),∴BC为: ![]() ;
;
①当点F落在BC边上时,如图2,作DM⊥y轴于M,FN⊥y轴于N.在△DEM与△EFN中,  ,∴△DEM≌△EFN(AAS),∴NF=EM=n﹣4,EN=DM=3
,∴△DEM≌△EFN(AAS),∴NF=EM=n﹣4,EN=DM=3
∴F为(n﹣4,n﹣3)
∴n﹣3=﹣![]() (n﹣4)+8,∴n=
(n﹣4)+8,∴n=![]() ;
;
②当点G落在BC边上时,如图3,作DM⊥y轴于M,GN⊥DM轴于N,由①同理可得△DEM≌△GDN,∴GN=DM=3,DN=EM=n﹣4,∴点G纵坐标为1,∴![]() ,∴x=14,∴DN=14+3=17=n﹣4,∴n=21;
,∴x=14,∴DN=14+3=17=n﹣4,∴n=21;
③当点F落在AB边上时,如图4,作DM⊥y轴于M,由①同理可得△DEM≌△EFO,∴OE=DM=3,即n=3;
④当点G落在AC边上时,如图5.∵∠CDE=∠AOC=90°,∠DCE=∠OCA,∴△DCE∽△OCA,∴![]() ,∴
,∴![]() ,∴n=
,∴n=![]() ,显然,点G不落在AB边上,点F不落在AC边上,故只存在以上四种情况.
,显然,点G不落在AB边上,点F不落在AC边上,故只存在以上四种情况.
综上可得,当n=![]() 或21或3或
或21或3或![]() 时,正方形的顶点F或G落在△ABC的边上.
时,正方形的顶点F或G落在△ABC的边上.


科目:初中数学 来源: 题型:
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
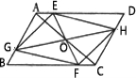
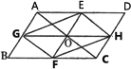
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“五一”小长假期间,某学校团委要求学生参加一项社会调查活动,八年级学生小明想了解他所居住的小区500户居民的家庭收入情况,从中随机调查了本小区一定数量居民家庭的收入情况(收入取整数,单位:元),并将调查的数据绘制成如下直方图和扇形图,根据图中提供的信息,解答下列问题:
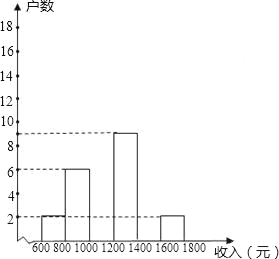
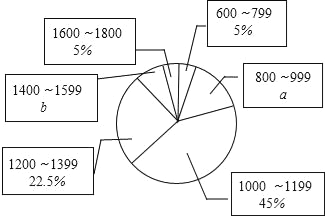
(1)这次共调查了 个家庭的收入,a= ,b= ;
(2)补全频数分布直方图,样本的中位数落在第 个小组;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
(4)在第1组和第5组的家庭中,随机抽取2户家庭,求这两户家庭人均月收入差距不超过200元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上,求M′的坐标;
(3)已知点C(﹣1,3),D(4,3),点N(x,y)和它的“n级关联点”N′都位于线段CD上,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年9月世界计算机大会在湖南省长沙市开幕,大会的主题是“计算万物,湘约未来”.从心算、珠算的古老智慧到“银河”“天河”“神威”创造的中国速度,“中国计算”为世界瞩目.超级计算机“天河一号”的性能是4700万亿次,换算成人工做四则运算,相当于60亿人算一年,它1秒就可以完成.数4700万亿用科学记数法表示为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
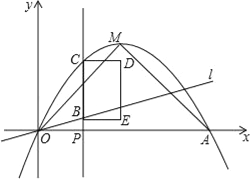
【题目】如图,抛物线y=﹣![]() x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=![]() x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东妈妈准备购买若干个粽子和咸鸭蛋(每个棕子的价格相同,每个咸鸭蛋的价格相同).已知某超市粽子的价格比咸鸭蛋的价格贵1.8元,小东妈妈发现,花30元购买粽子的个数与花12元购买的咸鸭蛋个数相同.
(1)求该超市粽子与咸鸭蛋的价格各是多少元?
(2)小东妈妈计划购买粽子与咸鸭蛋共18个,她的一张购物卡上还有余额40元,若只用这张购物卡,她最多能购买粽子多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
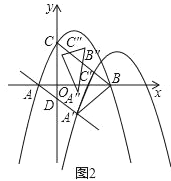
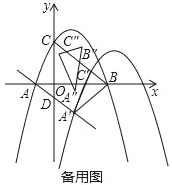
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮两人从甲地出发,沿相同的线路跑向乙地,小明先跑一段路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,两人一起以小明原来的速度跑向乙地,如图是小明、小亮两人在跑步的全过程中经过的路程y(米)与小明出发的时间x(秒)的函数图象,请根据题意解答下列问题:
(1)在跑步的全过程中,小明共跑了 米,小明的速度为 米/秒.
(2)求小亮跑步的速度及小亮在途中等候小明的时间;
(3)求小亮出发多长时间第一次与小明相遇?
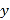
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com