
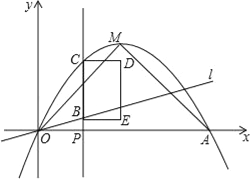
【题目】如图,抛物线y=﹣![]() x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=
x2+2x的顶点为M,与x轴交于0,A两点,点P(a,0)是线段0A上一动点(不包括端点),过点P作y轴的平行线,交直线y=![]() x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
x于点B,交抛物线于点C,以BC为一边,在BC的右侧作矩形BCDE,若CD=2,则当矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是__.
【答案】![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.
【解析】∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣4)2+4,∴顶点M的坐标为(4,4),
(x﹣4)2+4,∴顶点M的坐标为(4,4),
令y=0,则﹣![]() x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
x2+2x=0,整理得,x2﹣8x=0,解得x1=0,x2=8,∴点A的坐标为(8,0),
设直线AM的解析式为y=kx+b(k≠0),则![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+8,∴∠MAO=45°,由抛物线的对称性得,△AMO是等腰直角三角形,
①矩形BCDE为正方形时,BC=DC,∴(﹣![]() a2+2a)﹣
a2+2a)﹣![]() a=2,解得a1=
a=2,解得a1=![]() ,a2=
,a2=![]() ;
;
②矩形BCDE关于抛物线对称轴对称时,点P的横坐标a=4+![]() CD=4+
CD=4+![]() ×2=4+1=5;
×2=4+1=5;
③如图,点E在AM上时,设直线y=![]() x与直线AM相交于点G,
x与直线AM相交于点G,
联立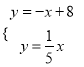 ,解得
,解得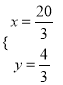 ,∴点G的坐标为(
,∴点G的坐标为(![]() ,
, ![]() ),
),
∵PB∥y轴,四边形BCDE为矩形,∴BE∥x轴,∴△GBE∽△OGA,
∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
过点G作GH⊥x轴于H,则GH∥PB,∴△OBP∽△OGH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得PB=1,∴点B的纵坐标为1,
,解得PB=1,∴点B的纵坐标为1,
代入y=![]() x得,
x得, ![]() x=1,解得x=5,∴点P的横坐标a=5,
x=1,解得x=5,∴点P的横坐标a=5,
∴从此位置到点B与点G重合,重叠部分为等腰直角三角形,∴![]() <a≤5;
<a≤5;
综上所述,矩形BCDE与△OAM重叠部分为轴对称图形时,a的取值范围是: ![]() 或
或![]() 或5或
或5或![]() <a<5,故答案为
<a<5,故答案为![]() 或
或![]() 或
或![]() <a≤5.
<a≤5.


科目:初中数学 来源: 题型:
【题目】有下列7个数
+4,﹣|﹣2|,-20%,![]() ,0,-(-1),3.14
,0,-(-1),3.14
(1)画出数轴,并将上面的七个数表示在数轴上;
(2)下图的两个圈的交叉部分表示什么数的集合,请填写在横线上,并把七个数中适合的数填写到两个圈的交叉部分.
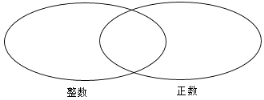
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() (
(![]() )与直线
)与直线![]() 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点A,B,C 在数轴上,对应表示的数是a,b,c.
![]()
(1)填空:A、B 之间的距离为 ;B、C 之间的距离为 ;A、C 之间的距离为 ;
(2)化简:|a+b|-|c-b|-|b-a|+|c|
(3)若 c2=9,-b 的倒数是它本身,a 的绝对值是 2,求(2a+b)-(c-b)-(a+2b-3c)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
分别交x轴,y轴于点A,C,点D(m,4)在直线AC上,点B在x轴正半轴上,且OB=2OC.点E是y轴上任意一点,连结DE,将线段DE按顺时针旋转90°得线段DG,作正方形DEFG,记点E为(0,n).
(1)求点D的坐标;
(2)记正方形DEFG的面积为S,
① 求S关于n的函数关系式;
② 当DF∥x轴时,求S的值;
(3)是否存在n的值,使正方形的顶点F或G落在△ABC的边上?若存在,求出所有满足条件的n的值;若不存在,说明理由.
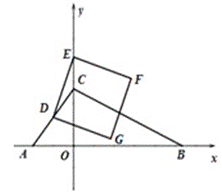
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=![]() 的图象经过点C(3,m).
的图象经过点C(3,m).
(1)求菱形OABC的周长;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1,点![]() ,
,![]() 表示的数互为相反数,结合数轴回答下列问题:
表示的数互为相反数,结合数轴回答下列问题:
![]()
(1)请在数轴上标出原点![]() 的位置.
的位置.
(2)直接写出点![]() ,
,![]() ,
,![]() ,
,![]() 所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
所表示的数,并判断哪一点表示的数的平方最大,最大是多少?
(3)从A,B两题中任选一题作答.
A. ①若点![]() 在数轴上,与点
在数轴上,与点![]() 的距离
的距离![]() ,求点
,求点![]() 表示的数;
表示的数;
②设动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点
出发,以每秒3个单位长度的速度沿数轴的正方向匀速向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
B.设点![]() ,
,![]() 都从点
都从点![]() 出发沿数轴的正方向匀速向终点
出发沿数轴的正方向匀速向终点![]() 运动.点
运动.点![]() 的速度为每秒2个单位长度,点
的速度为每秒2个单位长度,点![]() 的速度为每秒5个单位长度,当点
的速度为每秒5个单位长度,当点![]() 运动到点
运动到点![]() 时点
时点![]() 开始运动,设点
开始运动,设点![]() 运动的时间为
运动的时间为![]() 秒,求点
秒,求点![]() ,
,![]() 之间的距离
之间的距离![]() .(用含
.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形纸片OABC的顶点A,C分别在x轴,y轴的正半轴上,将纸片沿过点C的直线翻折,使点B恰好落在x轴上的点B′处,折痕交AB于点D.若OC=9,![]() ,则折痕CD所在直线的解析式为____.
,则折痕CD所在直线的解析式为____.
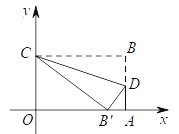
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,
![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)如图1,若![]() 为等腰直角三角形,求直线
为等腰直角三角形,求直线![]() 的函数解析式;
的函数解析式;
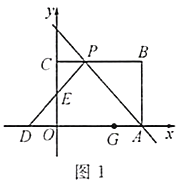
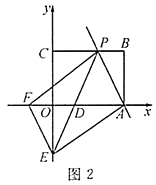
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若四边形
,若四边形![]() 是平行四边形,求直线
是平行四边形,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com