
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
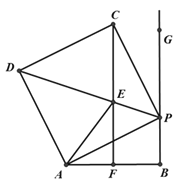
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
【答案】(1)△AEP≌△CEP;(2)垂直 ; 理由见详解; (3)20 .
【解析】
(1)四边形APCD正方形,则DP平分∠APC,PC=PA,∠APD=∠CPD=45°,即可求解;(2)△AEP≌△CEP,则∠EAP=∠ECP,而∠EAP=∠BAP,则∠FCP+∠CMP=90°,则∠AMF+∠PAB=90°。(3)证明△PCN≌△APB(AAS),则CN=PB=BF,PN=AB,即可求解。
证明:(1)∵四边形APCD正方形,
∴DP平分∠APC, PC=PA,
∴∠APD=∠CPD=45°,
在△AEP和△CEP
PC=PA
∠APD=∠CPD
PE=PE
∴△AEP≌△CEP(SAS).
(2) CF⊥AB.
理由如下: ∵△AEP≌△CEP,
∴∠EAP=∠ECP,
∵∠EAP=∠BAP.
∴∠BAP=∠FCP,
∵∠FCP+∠CMP=90°,∠AMF=∠CMP,
∴∠AMF+∠PAB=90°,
∴∠AFM=90°,
∴CF⊥AB.
(3)过点 C 作CN⊥PB.可证得△PCN≌△APB,
∴ CN=PB=BF, PN=AB,
∵△AEP≌△CEP, ∴AE=CE,
∴AE+EF+AF
=CE+EF+AF
=BN+AF
=PN+PB+AF
=AB+CN+AF
=AB+BF+AF
=2 AB
=20.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,它们表示的有理数分别为
,它们表示的有理数分别为![]() 、
、![]() 、
、![]() .已知
.已知![]() 是最大的负整数,且
是最大的负整数,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点表示的有理数分别是多少?
三点表示的有理数分别是多少?
(2)填空:
①如果数轴上点![]() 到
到![]() ,
,![]() 两点的距离相等,则点
两点的距离相等,则点![]() 表示的数为 ;
表示的数为 ;
②如果数轴上点![]() 到点
到点![]() 的距离为1,则点
的距离为1,则点![]() 表示的数为 ;
表示的数为 ;
(3)在数轴上是否存在一点![]() ,使点
,使点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的3倍?若存在,请求出点
的距离的3倍?若存在,请求出点![]() 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
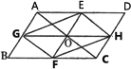
【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
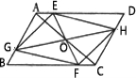
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
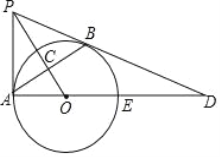
【题目】如图,PB与⊙O相切于点B,过点B作OP的垂线BA,垂足为C,交⊙O于点A,连结PA,AO,AO的延长线交⊙O于点E,与PB的延长线交于点D.
(1)求证:PA是⊙O的切线;
(2)若tan∠BAD=![]() ,且OC=4,求BD的长.
,且OC=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……照此规律,图A6比图A2多出“树枝”( )
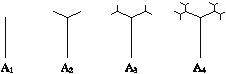
A.32个B.56个C.60个D.64个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“五一”小长假期间,某学校团委要求学生参加一项社会调查活动,八年级学生小明想了解他所居住的小区500户居民的家庭收入情况,从中随机调查了本小区一定数量居民家庭的收入情况(收入取整数,单位:元),并将调查的数据绘制成如下直方图和扇形图,根据图中提供的信息,解答下列问题:
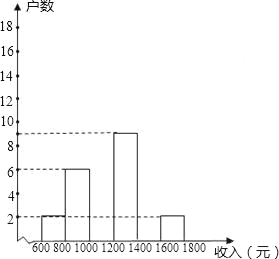
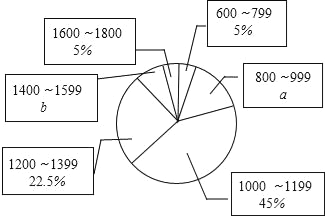
(1)这次共调查了 个家庭的收入,a= ,b= ;
(2)补全频数分布直方图,样本的中位数落在第 个小组;
(3)请你估计该居民小区家庭收入较低(不足1000元)的户数大约有多少户?
(4)在第1组和第5组的家庭中,随机抽取2户家庭,求这两户家庭人均月收入差距不超过200元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上,求M′的坐标;
(3)已知点C(﹣1,3),D(4,3),点N(x,y)和它的“n级关联点”N′都位于线段CD上,请直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
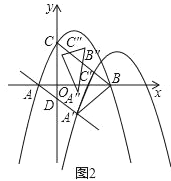
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD∥BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
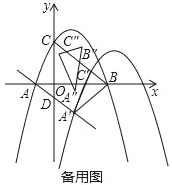
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作A′、C′,当△A′C′B是以C′B为底边的等腰三角形时,将等腰△A′C′B绕点D逆时针旋转一周,记旋转中的△A′C′B为△A″C″B′,若直线A″C″与y轴交于点K,直线A″C″与直线AD交于点I,当△DKI是以KI为底边的等腰三角形时,求出DK2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com