
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,它们表示的有理数分别为
,它们表示的有理数分别为![]() 、
、![]() 、
、![]() .已知
.已知![]() 是最大的负整数,且
是最大的负整数,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点表示的有理数分别是多少?
三点表示的有理数分别是多少?
(2)填空:
①如果数轴上点![]() 到
到![]() ,
,![]() 两点的距离相等,则点
两点的距离相等,则点![]() 表示的数为 ;
表示的数为 ;
②如果数轴上点![]() 到点
到点![]() 的距离为1,则点
的距离为1,则点![]() 表示的数为 ;
表示的数为 ;
(3)在数轴上是否存在一点![]() ,使点
,使点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的3倍?若存在,请求出点
的距离的3倍?若存在,请求出点![]() 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.
![]()
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
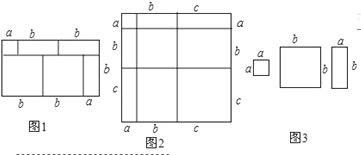
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店准备购进甲、乙两种图书共100本,购书款不高于1118元,预这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如表所示:
甲种图书 | 乙种图书 | |
进价(元/本) | 8 | 14 |
售价(元/本) | 18 | 26 |
请回答下列问题:
(1)书店有多少种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?(请你用所学的一次函数知识来解决)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□OABC的三个顶点分别为O(0,0),C(4,0),B(3,3),∠AOC的平分线OP交AB于点P,则点P的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次3个数:2、9、7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2、7、9、-2、7,这称为第1次操作,做第2次同样的操作后也可以产生一个新数串:2、5、7、2、9、-11、-2、9、7,继续依次操作下去,问从数串2、9、7开始操作第20次后所产生的那个数串的所有数之和是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

(1)这8筐白菜中,最接近25千克的那筐白菜为______千克;
(2)以每筐25千克为标准,这8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
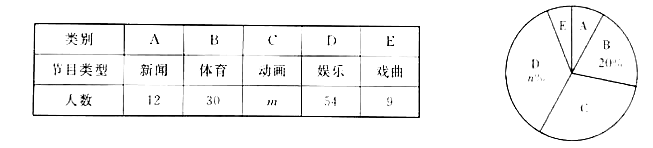
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中![]() 的值为 ,统计图中
的值为 ,统计图中![]() 的值为 ;
的值为 ;
(3)在统计图中,![]() 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=10,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且C、D与点B在AP两侧,在线段DP取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
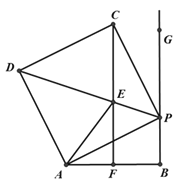
(1)求证:△AEP![]() △CEP;
△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com