
【题目】已知ac>0,a+b<0,且|c|>|b|,数轴上a、b、c对应的点是A、B、C.
(1)若|a|=a时,请在数轴上标出点A、B、C的大致位置;
(2)在(1)的条件下,化简:|a+b|+|b+c|﹣|c﹣a|.
![]()
【答案】(1)在数轴上表示对应点A、B、C如图所示,见解析;(2)|a+b|+|b+c|﹣|c﹣a|==0.
【解析】
(1)根据|a|=a,ac>0,a+b<0,可知a>0,c>0, b<0,|b|>|a|,结合|c|>|b|,即可在数轴上标出点A、B、C的大致位置;
(2)根据数轴上a、b、c的正负及大小关系,可知![]() ,求绝对值后,合并同类项,即可.
,求绝对值后,合并同类项,即可.
(1)∵ac>0,|a|=a,
∴a>0,c>0,
∵a+b<0,
∴b<﹣a<0,|b|>|a|,
∵|c|>|b|,
∴|c|>|b|>|a|,
∴OC>OB>OA,
∴在数轴上表示对应点A、B、C如下图所示,
![]()
(2)根据数轴上a、b、c的正负及大小关系,得:![]()
∴|a+b|+|b+c|﹣|c﹣a|=﹣a﹣b+b+c﹣(c﹣a)=0.


科目:初中数学 来源: 题型:
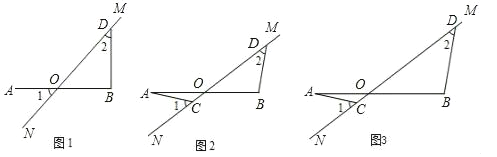
【题目】在图1至图3中,直线MN与线段AB相交于点O,∠1=∠2=45°.
(1)如图1,若AO=OB,请写出AO与BD的数量关系和位置关系;
(2)将图1中的MN绕点O顺时针旋转得到图2,其中AO=OB.求证:AC=BD,AC⊥BD;
(3)将图2中的OB拉长为AO的k倍得到图3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次3个数:2、9、7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2、7、9、-2、7,这称为第1次操作,做第2次同样的操作后也可以产生一个新数串:2、5、7、2、9、-11、-2、9、7,继续依次操作下去,问从数串2、9、7开始操作第20次后所产生的那个数串的所有数之和是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
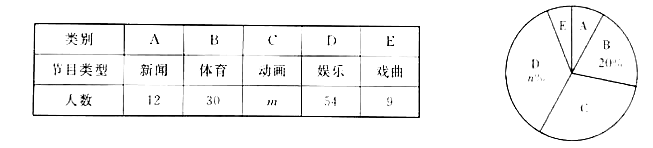
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中![]() 的值为 ,统计图中
的值为 ,统计图中![]() 的值为 ;
的值为 ;
(3)在统计图中,![]() 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
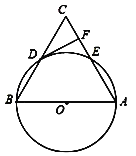
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列7个数
+4,﹣|﹣2|,-20%,![]() ,0,-(-1),3.14
,0,-(-1),3.14
(1)画出数轴,并将上面的七个数表示在数轴上;
(2)下图的两个圈的交叉部分表示什么数的集合,请填写在横线上,并把七个数中适合的数填写到两个圈的交叉部分.
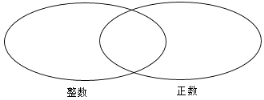
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD的外侧作等腰△ABE,AE=BE,连接ED、EC.
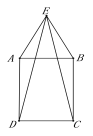
(1)求证:ED=EC.
(2)用无刻度的直尺作出△EDC中DC边上的高EH.(不写作法,保留作图的痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点A,B,C 在数轴上,对应表示的数是a,b,c.
![]()
(1)填空:A、B 之间的距离为 ;B、C 之间的距离为 ;A、C 之间的距离为 ;
(2)化简:|a+b|-|c-b|-|b-a|+|c|
(3)若 c2=9,-b 的倒数是它本身,a 的绝对值是 2,求(2a+b)-(c-b)-(a+2b-3c)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com